PDF

Int J Biol Sci 2007; 3(5):303-317. doi:10.7150/ijbs.3.303 This issue Cite

Review

The Forces Behind Cell Movement

Revathi Ananthakrishnan^{1 *}, Allen Ehrlicher²

1. Laboratory for Cell and Computational Biology, 1 Shields Avenue, University of California at Davis, Davis, CA-95616, USA.
2. Institute for Soft Matter Physics, Linne Strasse 5, Univ. of Leipzig, Leipzig, Germany-04103
* Present address: 3 Everett St, #3, Cambridge, MA-02138.

Abstract

Cell movement is a complex phenomenon primarily driven by the actin network beneath the cell membrane, and can be divided into three general components: protrusion of the leading edge of the cell, adhesion of the leading edge and deadhesion at the cell body and rear, and cytoskeletal contraction to pull the cell forward. Each of these steps is driven by physical forces generated by unique segments of the cytoskeleton. This review examines the specific physics underlying these phases of cell movement and the origins of the forces that drive locomotion.

Keywords: cell movement, crawling, motility, actin, polymerization, adhesion force, retraction force

1. Introduction

Cell movement or motility is a highly dynamic phenomenon that is essential to a variety of biological processes such as the development of an organism (morphogenesis), wound healing, cancer metastasis and immune response. For example, during morphogenesis there is a targeted movement of dividing cells to specific sites to form tissues and organs. For wound healing to occur, cells such as neutrophils (white blood cells) and macrophages (cells that ingest bacteria) move to the wound site to kill the microorganisms that cause infection, and fibroblasts (connective tissue cells) move there to remodel damaged structures [1]. In all these examples, cells reach their target by crawling. There are also other kinds of motility, such as the swimming of most sperm cells, and the movement of some bacteria by the rotation of flagellar motors [1]. Cell crawling, however, is the common mechanism employed by most motile eukaryotic animal cells [1], and is the focus of this review.

Although cell movement was observed as early as 1675 when van Leeuwenhoek saw cells crawl across his microscope slide, the molecular mechanisms behind cell movement have become a scientific focus only in the past few decades. Advances in fluorescence microscopy, molecular biology and biochemistry have enabled the discovery of the processes underlying motility and the identification of the major proteins behind these processes. These experimental techniques alone, however, cannot adequately explain whether these proteins are capable of generating the required forces for motility nor the physical mechanisms employed. A significant advance in this direction was made when biophysical studies helped identify regions where different force generating proteins are located, measured (in vitro) the exact forces generated by some of these proteins [2-6], and measured (in vivo) the forces associated with movement [7-9]. Theoretical studies and computational modeling have complemented the experimental work and have helped quantify how the proposed mechanisms and the forces generated at a molecular level are integrated to produce whole cell movement. This review describes the present state of knowledge gained from these experimental and theoretical studies on cell movement, with an emphasis on the physical basis of the forces that govern the crawling of single cells. It also references several websites with animations and movies, given in footnotes, to clarify the processes described.

As a cell moves on a substrate (the extracellular matrix if the cell moves inside an organism or a cover slide if it moves outside an organism), it experiences external forces, which include the viscous force or resistance from the surrounding medium and cell-substrate interaction forces, and internal forces that are generated by the cytoskeleton. In most animal cells, the cytoskeleton is the essential component in creating these motility-driving forces, and in coordinating the entire process of movement. The cytoskeleton is a polymer network, composed of three distinct biopolymer1 types: actin, microtubules and intermediate filaments. These biopolymers are differentiated principally by their rigidity, which can be described by the persistence length L_p. The persistence length is defined as the distance over which the filament is bent by thermal forces, and increases with increasing stiffness [10].

Actin filaments (AFs) are semiflexible polymers with L_p ~17 µm [11]. They are ~7 nm in diameter, are built from dimer pairs of globular actin monomers, and are functionally polar in nature [1,12]. This means that they have two distinct ends: a fast and a slow growing end (called the plus end and minus end respectively) [1,12]. The minus end has a critical actin monomer concentration that is ~6 times higher than that at the plus end (~0.6 μM and ~0.1 μM at the minus and plus end respectively). When the end of an AF is exposed to a concentration of monomeric actin that is above its critical concentration, the filament end binds monomers and grows by polymerization. Conversely, when the concentration is below the critical concentration, monomers detach from the filament end, and the filament shrinks by depolymerization. Simply by having these two different critical actin concentrations at the opposing ends of the filament, AFs can grow asymmetrically, and when the actin monomer concentration lies between the two values, only the plus end grows while the minus end shrinks. This process, where the length of the filament stays roughly constant and the polymerized monomers within the AF transfer momentum forward due to asymmetric plus end polymerization, is known as treadmilling; it is a critical aspect of how polymerizing AFs can generate force. Microtubules (MTs) are the stiffest of the biopolymers, with L_p ranging from 100 to 5000 µm depending on the filament length [13]. MTs are rod-like polymers, with an outer diameter of ~25 nm. Tubulin protein subunits assemble into protofilaments, and typically 13 of these protofilaments then align to form a hollow tube, imbuing MTs with their incredible rigidity. MTs exhibit similar dynamics to those of actin: they are functionally polar, treadmill, and can impart a force through polymerization [14]. Intermediate filaments (IFs) are much more flexible than AFs and MTs (L_p~0.3-1.0 µm). They range in diameter from 8 to12 nm, between that of AFs and MTs. There are different classes of IFs such as vimetin, desmin, keratin, lamin and neurofilaments, with different cell types having different IFs. Unlike AFs or MTs, IFs are not polarized, do not treadmill, do not generally depolymerize under physiological conditions once polymerized [15], and are therefore considered to be more static in nature than AFs and MTs.

These three kinds of biopolymers build an internal cellular scaffold, known as the cytoskeleton − an organized and coherent structure that is formed by connecting these filaments via entanglements, and also crosslinking, bundling, binding, motor and other proteins. These cytoskeletal assemblies then work together as a composite, dynamic material in cell functions such as structural integrity, shape, division, and organelle transport and cell motility. With respect to motility, although the other polymer assemblies in the cell also aid in coordinating movement and powering translocation, the actin cytoskeleton is regarded as the essential engine that drives cell protrusion [16, 17], the first step of movement. It is also integral to achieving the two other steps of movement: adhesion of the leading edge and deadhesion at the cell body and rear, and translocation of the bulk of the cell. The actin cytoskeleton is highly dynamic and the actin structures in the cell can be readily reorganized by the cell to adapt their behavior for movement according to the surrounding environment. The constant restructuring of the actin cytoskeleton and the transition from one actin structure to another is vital in enabling the cell to change its elastic properties rapidly, and this dynamic response is fundamental for movement.

AFs in vivo can assemble into different structures such as networks and bundles. Mesh-like actin networks consisting of short crosslinked AFs are primarily found at the leading edge of cells [9]. The growth of these meshworks i.e. the continuous creation of new actin network at the leading edge is considered to be essential for pushing the cell forward. This network formation is carried out with the help of numerous accessory proteins [18]. Activating proteins (e.g. WASp) enable nucleator proteins (e.g. arp2/3 complex) to initiate the polymerization and assembly of new actin filaments. Actin depolymerization promoting proteins (e.g. cofilin) can also aid network growth. Cofilin (also known as Actin Depolymerizing Factor ADF) severs actin filaments and creates new plus ends for the growth of new actin filaments. Actin binding proteins (e.g. profilin, thymosineβ-4) maintain a steady actin monomer pool for polymerization, while crosslinking and bundling proteins (e.g. filamin, α-actinin, fascin) help form connected actin networks. Capping proteins (e.g. CapZ) control filament length by attaching to actin filament ends and stopping further polymerization, while severing and fragmenting proteins (e.g. gelsolin, severin) cut actin filaments and networks. All these proteins work together to coordinate actin network formation and bring about leading edge motility in several steps, as described previously (such as in Figure No. 2 of Pollard 2000 [18], which shows the Dendritic Nucleation Model for movement of leading edge, or Figure No. 3 of Pollard 2003 [19]).

Actin bundles are composed of parallel arrays of individual AFs that are closely packed and crosslinked by proteins such as fascin, fimbrin and scruin, and fulfill structural and sensory roles that are key to cell movement. Often, these actin bundles connect distal points of adhesion, allowing tension to be propagated across the cell, and enabling the cell to apply forces on the substrate and move. They are appropriately known as stress fibers, distributing forces and positively reinforcing adhesion sites [9]. In some cells, actin bundles known as filopodia may extend out beyond the lamellar edge, and function as chemical and mechanical sensors, and aid the cell in migrating through tissue [20,21].

AFs also generate motility forces through interactions with myosin motors. Myosin motors consist of a head, neck, and tail region; while some myosin motors have one head and neck, others have two. The head/neck region is responsible for attachment and force production, while the tail region is principally believed to be for connecting to cargo, such as other myosins, vesicles, or filaments. Myosin motors do work on actin filaments through a general three-step process of binding, power stroke, and unbinding [1,12]. This process is continuously repeated, and leads to the generation of a contractile force (acto-myosin contractile force) thought to be essential in pulling the bulk of the cell forward during movement.

In most cell types, the microtubules predominantly extend radially from the centrosome to the actin network at the cell periphery, with their plus ends towards the cell edge, and thus display a hub and spoke arrangement. These microtubules aid in determining the direction of cell movement [22].

Intermediate filaments create a fibrous network that spans the cell interior and connects the nucleus to the cell membrane, providing structural integrity to cells. Due to their more static properties, it has long been held that IFs are of little importance for cell movement [12], since cell movement requires the cytoskeleton to be dynamic and to reorganize rapidly; although IFs may not be critical to cell movement, recent work shows IFs to be more dynamic than previously thought [23].

2. The Process of Cell Movement

A cell begins to move in response to an external signal in its surrounding environment. This can be a physical, chemical, diffusible or non-diffusible signal that is detected by receptor proteins located on the cell membrane, and transmitted by them via signaling cascades to the cell interior [1]. A cell, such as a white blood cell, yeast cell or slime mold cell, is believed to sense the signal direction by spatially recognizing external gradients (receptor proteins become more concentrated on the side of the cell where the signal is present) [24].

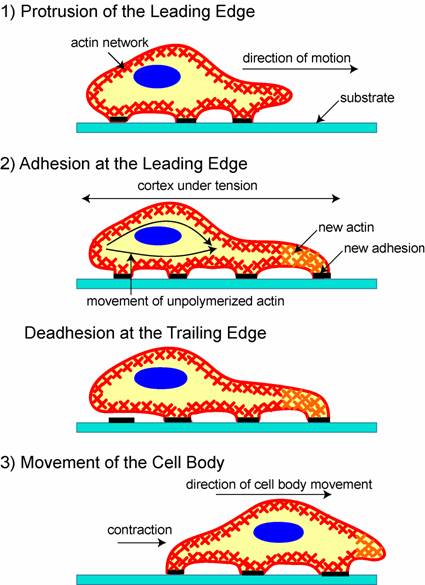
Once cell movement begins, the process, which involves the constant restructuring of the actin cytoskeleton, can be divided into three stages in most cells (Figure 1) [25]. First, a cell propels the membrane forward by orienting and reorganizing (growing) the actin network at its leading edge. Second, it adheres to the substrate at the leading edge and deadheres (releases) at the cell body and rear of the cell. Finally, contractile forces, generated largely by the action of the acto-myosin network, pull the cell forward.

After sensing the signal, the cell starts moving in response to the signal by polymerizing actin. If the signal is a chemoattractant, for example, actin polymerizes in the region of the cell closest to the signal, whereas if the signal is a chemorepellant, the cell moves away by polymerizing actin in the opposite side. As the extending edge moves forward, the cell constantly monitors the signal direction and tailors its direction of motion accordingly. This signal tracking is beautifully demonstrated by a cell that chases an object it attempts to engulf2 or by a cell that moves in response to a chemoattractant3.

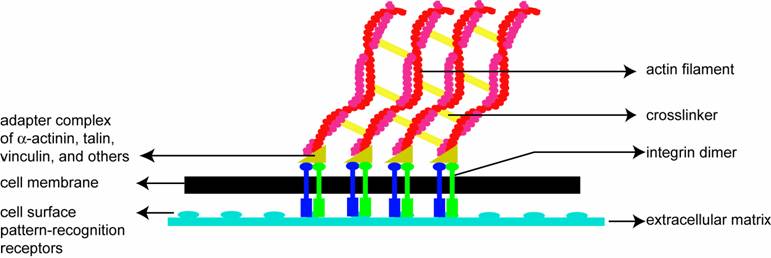
Soon after the leading edge begins to protrude, adhesion molecules gathered in the extending region help attach the leading edge to the substrate. Cell-substrate attachments are created at the leading edge when actin bundles link the cytoskeleton to the substrate at certain sites via adhesion molecules (Figure 2). These attachments prevent the protruding leading edge from retracting. As the cell continues to adhere at the leading edge, it deadheres at the cell body and rear of the cell, possibly by the disassembly or contraction of its attachments (actin bundles).

Finally, the rest of the cell is pulled forward, mainly by contractile forces that are produced by myosin motors sliding on actin filaments, which are in the cell body and at the rear.

All the stages or processes described above are continuously running as the cell moves on the substrate, with the actin cytoskeleton transitioning between a solid-like elastic material (gel) and a solution-like viscous material (sol). These transitions, called gel-sol transitions, are crucial for cell movement [26]. They are likely caused by the constant net actin polymerization and network assembly at the leading edge and depolymerization and disassembly at the rear of the cell. The transition of an actin network to a more fluid-like state may also be motor driven [27]. These processes lead to local changes in the elasticity of the cell as it moves.

In summary, the entire process of cell movement is coordinated spatially as well as temporally by many proteins via mechanical changes in the cytoskeletal structure and changes in the force production centers.

3. The Forces of Cell Movement

a) Polymerization Mechanics

The first step of cell movement is protrusion of the leading edge. Undoubtedly, propulsion of the leading edge is a multi-step, complex process [18-19, 28-33], but the basic active mechanism that is believed to move the leading edge is the polymerization of actin filaments towards the cell membrane. Polymerizing actin filaments alone, without any accompanying motors, can generate significant force to move a cell's leading edge. In addition, filament-substrate adhesions are required to prevent the backward movement of polymerizing actin filaments. How does a filament elongating against a load − in this case, the cell membrane and external load, if any − generate such a force?

There are two main types of models which have been proposed to explain force generation by actin polymerization (polymerization force): ratchet models [34,35], and autocatalytic models [36,37].

 Figure 1 

A schematic of the three stages of cell movement, based on [1,12]: after determining its direction of motion, the cell extends a protusion in this direction by actin polymerization at the leading edge. It then adheres its leading edge to the surface on which it is moving and de-adheres at the cell body and rear. Finally, it pulls the whole cell body forward by contracile forces generated at the cell body and rear of the cell.

 Figure 2 

A schematic (based on a figure in http://www.rpi.edu/dept/bcbp/molbiochem/MBWeb/mb2/part1/actin.htm) showing how the cell adheres to the substrate. Cell-substrate attachments are formed when actin bundles connect to the substrate at certain sites via adhesion molecules such as vinculin, talin and integrin.

The basic working principle of ratchet models can be described as follows. If the membrane were fixed and immovable, an actin filament would stop polymerizing when it bumped into it and would be unable to push against it or generate force. However, the membrane does not remain stationary but undergoes constant Brownian motion i.e. random thermal fluctuation due to the membrane's small size scale and relative flexibility. In addition, an actin filament is not a stiff, immovable rod that stops growing once it reaches the membrane but is an elastic filament that can bend in response to the load. If the bending of the filament away from the membrane is adequately large (angle > ~30°) and the filament is sufficiently long (> ~70 nm) but without buckling, an actin monomer (which is 2.7 nm in size) can easily insert itself between the filament and membrane4. The lengthened filament can subsequently apply an elastic force on the membrane and push it forward. Each addition of a monomer “ratchets” the membrane, which implies that this process prohibits backward movement of the membrane and ensures that there is only a net forward motion of the cell edge. This model, proposed to explain force generation by a single polymerizing actin filament, is called the Elastic Brownian Ratchet Model [34]. An extension of the Elastic Brownian Ratchet Model is the Tethered Elastic Brownian Ratchet Model which incorporates the transient attachment of actin filaments to the surface or membrane and considers two sets of filaments: working filaments, which are filaments that are not attached to the surface and can exert a force on it, and attached filaments, which cannot exert a force on the surface [35]. Attached filaments are converted to working filaments when they dissociate from the surface and working filaments are converted to non working (i.e. attached) filaments when they are capped. Based on the Dendritic-Nucleation Model and its branching mechanism, the Tethered Elastic Brownian Ratchet Model importantly assumes that new actin filaments/branches are generated independent of existing branches. Under this assumption, the model attempts to understand force generation from a population of filaments in an actin network.

Theoretical calculations, based on the above ratchet mechanism along with thermodynamic principles to find the energy of monomer addition to a polymer tip, can provide estimates for the maximum force generated by a single polymerizing actin filament. The maximum force that a filament can develop (stall force) is estimated by equating the work done to push a load through a distance δ to the energy required to add a monomer to the filament tip [38]. This is given by the thermodynamic expression F_max = (k_BT/ δ)ln(A_*k_on/k_off), where k_BT is thermal energy, δ is the size of an actin monomer, k_on and k_off are the association and dissociation constants for an actin monomer adding to or falling off from a polymer tip, and A is the monomeric actin concentration [38]. If typical values are substituted in the above equation for an actin filament and for the monomeric actin concentration in the cell, the maximum force generated by a single actin filament is 5-7 pN [38]. Although this calculation is simplistic, it can be used to estimate the force generated at the leading edge. Aggregating the predicted force of ~5-7 pN across the hundreds of actin filaments per micron thought to exist at the leading edge of a cell, an estimate for the polymerization force at the leading edge is several piconewtons per micron (or is on the order of nanonewtons per micron) [35] – a force large enough to tackle the membrane load or resistance [35] (note that membrane resistance is generated by the breaking of linkages between the actin cytoskeleton and the membrane by the growing actin network, and the membrane bending force).

However, as noted, the force calculations with the ratchet models do not include the role of motor proteins in generating force. Based on studies in the bacterial pathogen Listeria and other experimental systems, recent work by Dickinson and others [39] concludes that the forces predicted by the ratchet models alone are not sufficient to account for the observed polymerization forces in these systems. It shows that much larger forces can be generated by considering the action of motors at the tip of the actin filaments (end tracking motors), which can efficiently convert free energy into work even in the case of persistently tethered filaments.

The Autocatalytic Model also explores force generation by an actin filament and actin network. To understand force generation by a single filament, the model assumes that the load diffuses and that the probability of monomer addition to a polymer tip includes a Boltzmann factor [36], which is identical to the basis of the Elastic Brownian Ratchet Model. To study the problem of force generation by a network, two approaches have been used: a numerical approach that uses stochastic simulations of an actin network growing against a load, while tracking the positions and orientation of all actin filaments over time [36], and a deterministic approach that uses an explicit rate equation for filament orientation distribution [37]. Both approaches incorporate the main assumption that new actin branches are generated from existing branches, which differs from the assumption made in the Tethered Elastic Brownian Ratchet Model. The transient attachment of actin filaments to the surface is not considered in either approach of the Autocatalytic Model. The stochastic simulations are used to study the dependence of growth velocity on capping rate, load force, branching and other parameters. The simulations show that, for a fixed actin concentration, the growth velocity has an inverse linear relation with the capping rate and equals zero when the number of branches is less than 1.5 [36]. These simulations, however, could be performed only for a small parameter range that is computationally feasible. Hence, the deterministic model was developed to study a larger parameter range and test the generality of the previous numerical results rigorously [37]. In addition, the deterministic equations can be easily modified to accommodate the assumption that new branches are generated independent of existing branches, as assumed in the Tethered Elastic Brownian Ratchet Model. Hence by using the same basic set of equations, the predictions of the autocatalytic and ratchet models are compared in Carlsson 2003 [37].

One main prediction of these models (ratchet model and autocatalytic model) that can be used to compare them and experimentally test them is the relation between the load (force) against which a polymerizing actin filament (or network) elongates and the filament's (or network's) resultant growth velocity. For a single filament, the Elastic Brownian Ratchet Model predicts an exponential force-velocity relation V = V_max exp(-f*δ/k_BT) - V_dep, where V_max is the free polymerization velocity, f is the load force on a single filament, and V_dep is the depolymerization velocity (see [34] for derivation). It is not surprising that the Autocatalytic Model also predicts the same exponential force-velocity relation as the Elastic Brownian Ratchet Model for a single filament, given that the underlying basics of both models are the same in this case [36]. Although the single filament force-velocity relation is the same, the prediction for the force-velocity relation for a network growing against a load is very different from the Tethered Elastic Brownian Ratchet Model and the Autocatalytic Model due to the following main differences in assumptions: a) new branches are generated independent of existing branches in the Tethered Elastic Brownian Ratchet Model, while they are generated only from existing branches in the Autocatalytic Model, and b) only the working filaments generate force (opposing the load force and force from attached filaments) in the Tethered Elastic Brownian Ratchet Model, whereas all filaments generate force to oppose the load force in the Autocatalytic Model. The Tethered Elastic Brownian Ratchet Model predicts a biphasic force-velocity relation where the velocity decreases rapidly for small forces and decreases much more slowly for high forces [35]. A qualitative explanation for this predicted behavior from the Tethered Elastic Brownian Ratchet Model is that the network growth velocity depends on the ratio of working to attached filaments. In the model, the number of working filaments is independent of load, while the number of attached filaments is not independent of load due to the dependence of the dissociation rate of attached filaments on velocity. If the load is high and velocity is low, the dissociation rate decreases, leading to an increase in the number of attached filaments and a slow decrease in velocity [35]. On the other hand, the Autocatalytic Model predicts that the actin network growth velocity is independent of the applied force or load i.e. V= V₀ (see [36,37] for details). A qualitative explanation for the insensitivity of the velocity to the force in this case is that if the load increases, the number of filaments pushing the load also increases proportionately, leaving the force per filament and the growth velocity unchanged [37]. When the equations of the Autocatalytic Model are modified to accommodate the assumption of an independent growth of new branches, it yields a force-velocity relation that is qualitatively similar to that of the Tethered Elastic Brownian Ratchet Model [37]. However, the other underlying assumptions of the models and the reasons for arriving at the same result from these two network models are different [40]. It should also be noted that when the equations of the Tethered Elastic Brownian Ratchet Model are modified to accommodate branching as in the Autocatalytic Model, the analysis does not yield a force-velocity curve similar to that of the Autocatalytic Model but a biphasic result that is unchanged from that of the Tethered Elastic Brownian Ratchet Model itself [35]. This is likely due to the other differences between the models (point b) above as well as filament orientation (not incorporated in ratchet models) and branching rate (not considered explicitly in the Tethered Elastic Brownian Ratchet Model modified to accommodate autocatalytic branching [40]). The above results emphasize that the two models are fundamentally different models for force generation by an actin network [40].

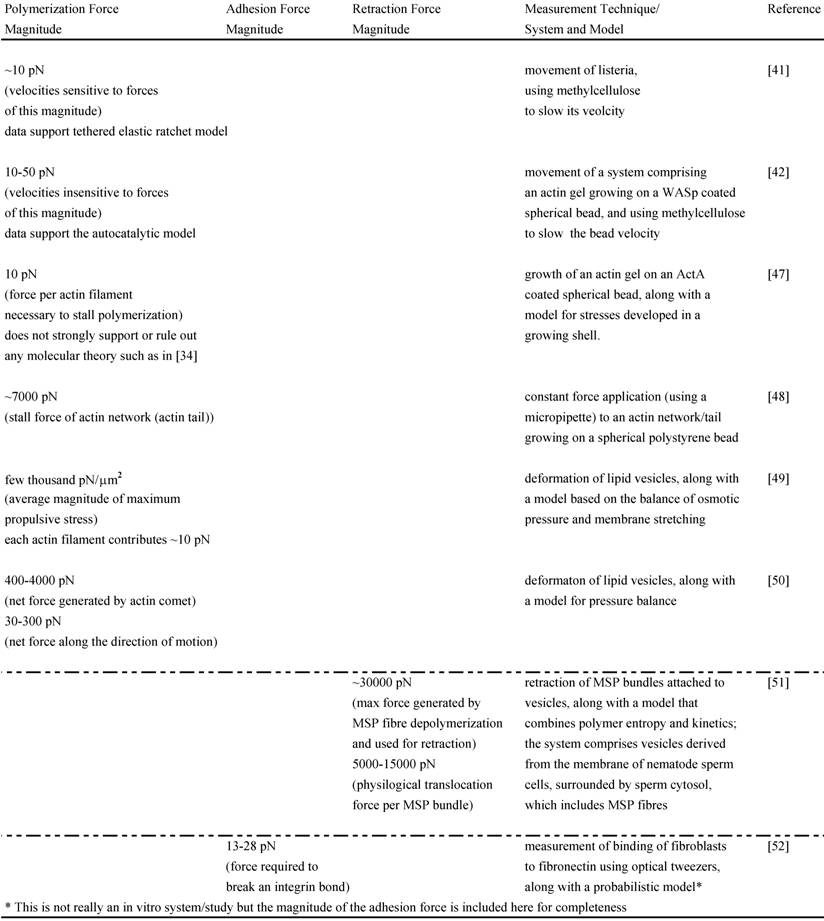
The force-velocity relations for networks from these two models have been tested experimentally in vitro. One in vitro study performed with Listeria used increasing amounts of methylcellulose to slow its velocity and computed the corresponding viscous resistive force exerted on the body in each case with the Stokes Equation, knowing the viscosity of methylcelluose, the velocity of bacterial motion and the shape factor of the bacterium. The analysis yielded force-velocity data that are quantitatively similar to that proposed by the Tethered Elastic Brownian Ratchet Model [41]. Another similar study was carried out in a biomimetic system (spherical polystyrene bead coated with WASp on which an actin gel grows in the presence of other purified proteins) [42]; it also used varying amounts of methylcellulose to slow the bead velocity and computed the force acting on the bead with the Stokes Equation. The study yielded force-velocity data that support the Autocatalytic model [42]. One reason for the different results of these two similar in vitro experiments may be that only the analysis of Wiesner and coworkers [42] incorporates the impact of methylcellulose on the force-velocity curve other than due to its viscosity effect alone. It is possible that this and other differing assumptions between the two studies lead to analyzing different regimes of the force-velocity curve (see [40] for further explanation) and to supporting different models. To shed further light on these models and the polymerization force, several other in vitro motility systems have also been designed (see Table 1) [43-48]. Neither model has been unambiguously favored as a result of these in vitro data. However, these studies still provide useful estimates of the polymerization forces such as the stall force of an actin filament, stall force of an actin comet/network, the maximum propulsive force generated by an actin network in the given in vitro system and the contribution of each actin filament to the total force measured. They also help us begin understanding and investigating the polymerization mechanics operating in vivo.

In vivo, it is not easy experimentally to test the derived single filament or actin network force-velocity relationships of these models and thus discern between the ratchet and autocatalytic network models [37]. It is also not easy theoretically to extend these models to that for the actin network at the leading edge. Several in vivo factors such as external load and membrane characteristics – membrane fluctuations and membrane load (resistance) – crucially determine the lamellipodial protrusion velocity, and need to be considered carefully similar to the detailed analysis that has been performed for filopodial protrusion [53]. Membrane resistance is, for example, an important factor that is postulated to restrain the growth (polymerization) of actin filaments at the leading edge and to determine the protrusion velocity [54]. Experimental studies have investigated the relation between membrane resistance and protrusion velocity by changing the membrane resistance in various ways and observing the protrusion velocity. Methods to change the membrane resistance include the use of detergents or fluorescent lipids to expand membrane area or an external force to stretch the membrane, all of which techniques reduce resistance, or the use of the microtubule disrupter nocodazole which contracts cells, or osmosis to swell cells, which techniques increase resistance [55,56]. The results of all these experiments clearly demonstrate an inverse relation between membrane resistance and protrusion velocity and estimate a membrane resistance force of ~30 pN/μm [55]. In one modeling study, membrane resistance is incorporated in a simple manner: the single filament force-velocity relation obtained from the Elastic Brownian Ratchet Model is extended to a large number of filaments pushing the membrane (as in the lamellipodium), assuming an uniform distribution of the membrane load (resistance) among the filaments; an expression for the cell's protrusion velocity is then derived [54]. The velocity is shown to be inversely proportional to membrane resistance, in agreement with the experimental results. However, such force-velocity predictions for the protruding cell still need further experimental validation in vivo.

In summary, the ratchet models [34, 35] and autocatalytic models [36,37] suggest likely molecular mechanisms of actin force generation and protrusion of the leading edge and discuss parameter regimes in which they could be applicable in vivo. Since all the parameters required to test the models are not yet available for the in vivo case, neither model has been either conclusively proved or ruled out in vivo, and their applicability to cell motility is still under investigation. Nevertheless, these models provide useful insights into understanding cell protrusion, since it is possible that the actual protrusion mechanism is a combination of the mechanisms advanced by both classes of models [37].

b) Adhesion Mechanics

The leading edge of the cell protrudes as a result of polymerization of the actin network in concert with adhesion of the extending network to the underlying substrate via integrins and other adhesion molecules. The exact distribution of cell-substrate attachments, the force with which the protruding cell adheres to the underlying substrate in various cell types, and changes or gradients in this adhesion force within the leading edge as one moves perpendicularly away from the tip of the leading edge are still active research areas. However, both the spatial distribution pattern of attachments and the adhesive force vary from cell type to cell type and are important factors that determine the protrusion rate and rate of translocation (rate at which the bulk of the cell/ cell body moves) of each cell type [57,58]. The adhesions near the cell's leading edge are crucially required to convert some of the polymerization force into protrusion; the rest of it contributes to the flow of the actin network. To understand what actin flow means, consider the case of a neuronal growth cone [59,16]. In this case, due to polymerization at the leading edge, the actin network there is pushed forward. At the same time, polymerizing actin filaments flow away from the leading edge at a fairly constant rate, known as centripetal actin flux or actin flow [60,61].

In many migrating cells, such as neuronal growth cones, fibroblasts, and fish keratocytes, the actin flow is modulated in a phenomenon known as retrograde flow, which is an important factor that determines the cell's translocation rate via the adhesion mechanics, as described in the section below. The term retrograde flow describes the variable movement of actin filaments rearward with respect to the substrate, and generally in a direction opposite to the movement of the cell [62-64]. Both actin polymerization and myosin motors are crucial in driving retrograde flow. While experimental studies on fibroblasts and dictyostellium have established that actin polymerization contributes to the generation of retrograde flow by providing a constant actin source and by pushing the lamellipodial actin network backward [65,66], the role of myosin motors in retrograde flow is still being studied as the essential myosin subtypes in many systems is unclear. Myosin motors are believed to generate retrograde flow by producing contractile cytoskeletal forces (inward pulling forces). Observations concerning myosin motors and retrograde flow include the following: myosin II motors have been revealed to play an essential role in generating retrograde flow in fish keratocytes [67]. Mysoin IIA, myosin IIB, and myosin Ic have been found to contribute to retrograde flow in neuronal growth cones, while myosin IIB and V have been found to contribute to growth cone spreading, highlighting the varied roles of myosin in growth cone movement [68-70]. Similarly, in fibroblasts, an important role for myosin IIA in retrograde flow and cell spreading has been identified, but both events are unaffected by the deletion of myosin IIB [71]. In summary, regarding movement and retrograde flow, all these studies indicate that both polymerization and molecular motors contribute critically to the generation of retrograde flow [72], but the extent of the contribution of polymerization versus that of myosin motors to retrograde flow may be different in different cell types.

 Table 1 

Magnitudes of various forces measured in vitro:

The association between the cell translocation rate and retrograde flow can be explained by the existence of a molecular clutch [73,64]. The molecular clutch is thought to be composed of vinculin, talin and other adhesion complexes, and determines the extent to which the cytoskeleton and underlying substrate are linked and can interact. Through this interaction, the clutch controls the transmission of the cytoskeletal contractile forces to the substrate, and the cell's translocation rate. When the clutch is engaged, there is an increase in the rate of translocation and a decrease in the retrograde flow because this tight cytoskeleton-substrate linkage enables an effective transmission of the acto-myosin contractile forces to the substrate via the adhesion complexes. It consequently enables the cell to move forward by pushing against the substrate with traction forces. The engaged clutch also allows the actin polymerization force to drive the cell forward efficiently. In contrast, when the clutch is not engaged, the loose coupling between the cystoskeleton and substrate results in an ineffective force transmission to the substrate; in this case, instead of the cell being moved forward efficiently, the actin meshwork is pushed backwards resulting in high retrograde flow and a low translocation rate. Thus, if we consider that the “wheels” (actin filament mesh) spin at a constant velocity (actin flow) but sometimes stick or slip on the road (variable traction of focal adhesions), we begin to see how the “clutch hypothesis” explains observations.

The clutch hypothesis thus predicts that slow moving cells (low translocation rate) have a high retrograde flow and generate less traction force, while in fast moving cells, a smaller retrograde flow and a larger traction force are expected. However, although many slow moving cells have been observed to have high retrograde flow and a large number of adhesions, they are also observed to generate large traction forces, which is in contrast to the above prediction. To explain this observation and to understand the relation between cell speed, traction forces and retrograde flow more clearly, several further studies have been performed recently [64, 74-78]. One of these studies on fish keratocytes [64] reveals that a phenomenon, called adhesion raking (i.e. the raking inward of the cytoskeleton against the substrate), can also produce retrograde flow and needs to be considered. When the clutch is engaged and raking occurs, the traction forces exerted on the substrate are large, but when the clutch is not engaged and retrograde flow is high, the traction forces are small (Figure 3). Since it is likely that both phenomena (adhesion raking and clutch disengagement) occur simultaneously in the cell, their combined effect produces a non-linear (biphasic) relation between cell speed and adhesiveness (the relation between cell speed and traction force is also thus non-linear) [64], a result in agreement with other experimental and computational studies on fibroblasts, neutrophils etc. [74-78]. Thus, the study concludes that when the adhesion to the substrate is too strong, the contractile machinery cannot function effectively to produce retraction and cell movement, whereas when it is too weak, the new adhesions that develop at the leading edge cannot establish themselves firmly enough to produce cell motion [64]. Hence, for rapid cell movement, the adhesion force needs to be optimum and retrograde flow minimum, while for slow movement, adhesion is below or above optimum and retrograde flow is high. Note that in most steady or smooth moving cells such as fish keratocytes, the cell's translocation rate and protrusion rate are identical. However, cells such as neuronal growth cones exhibit significant stochastic fluctuations in the protrusion velocity − due to variations in actin polymerization rates − that occur at a much smaller timescale than retrograde flow [16].

Many of the above studies [64,75] have analyzed retrograde flow using fluorescence speckle microscopy data on the assembly and disassembly of the actin network in conjunction with computational models [79]. In the technique of fluorescent speckle microscopy (FSM), a small number of proteins subunits of a macromolecule (actin, in this case) are labeled, and the movement of these fluorescent speckles is then recorded5. Betz and coworkers also analyzed retrograde flow rates in neuronal growth cones by tracking patterns in GFP-actin fluorescent growth cones [16]. All these studies produce accurate actin flow trajectories and velocities in vivo and have detected both protrusion of the leading edge and retrograde flow in most cell types, whose speeds and adhesion forces vary.

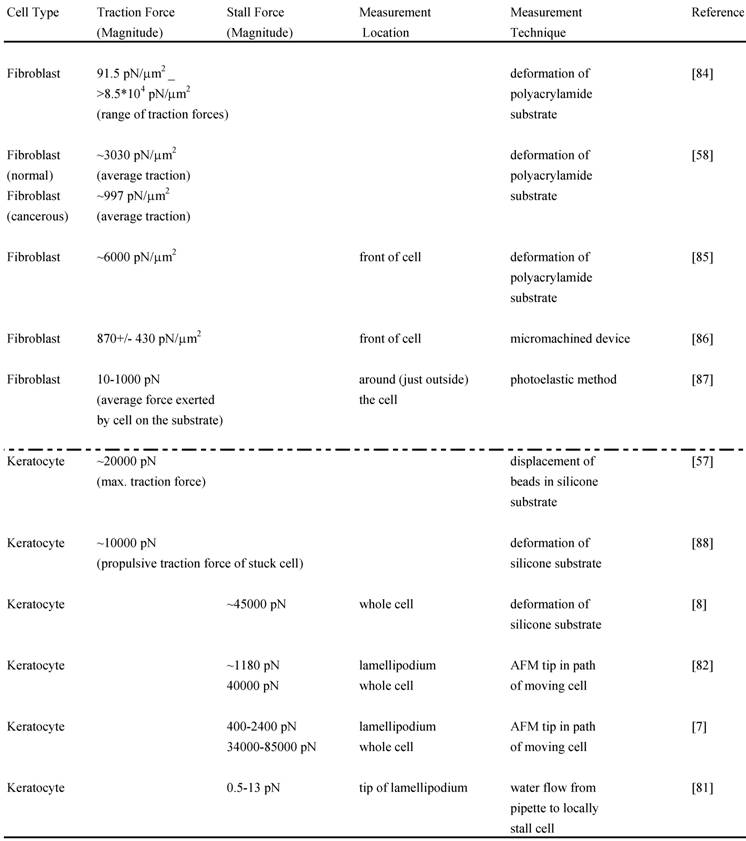
Although the adhesion force varies among cell types, estimates for the adhesion force at the leading edge can be obtained. Experiments performed to determine the adhesion force – the force required to break a single integrin attachment for example (see Figure 2 for integrin attachment) – yield a value of ~10-30 pN per attachment [80, 52]. In a recent study [81], the net adhesion force has been measured by applying a counter force of fluid flow (water flow from a pipette) to the leading edge of a moving fish keratocyte until the leading edge is locally stalled6. When the Navier-Stokes Equations for fluid flow are used to numerically estimate the force at the cell due to the water flow, the analysis yields the result that a force of only a few piconewtons causes the cell to lose adhesion and stop moving forward locally. Additionally, the analysis reveals that the actin polymerization is not stopped by this low force from the water flow but that the nascent adhesions at the tip of the leading edge are disrupted. As already mentioned, the maximum polymerization force that can be generated by a single elongating actin filament is estimated to be 5-7 pN. Since there are several actin filaments and integrin attachments per micron at the leading edge, the total force developed by the protruding leading edge is likely to be several nanonewtons. Two recent studies have directly measured the actin polymerization protrusive force and stall force by placing an Atomic Force Microscopy (AFM) cantilever tip in the path of a moving fish keratocyte and blocking its movement [7,82]. Both studies find effective lamellipodium polymerization pressures of ~ 1 kPa. Brunner and coworkers measured larger main cell body motility forces ranging from 34 to 85 nN [7]. These results [7,82] combined with those of Bohnet and coworkers [81] illustrate the importance of adhesion and its requirement for movement, since polymerization requires traction to produce cell movement, and must work synergistically and simultaneously with adhesion to drive motility. Various other groups have measured motility forces (traction, stall forces) for a variety of cell types using different techniques, such as deformable elastic substrates (e.g. silicone membranes), force sensor arrays and cell traction force microscopy (see Relation Among Force and also recent review [83]) and some of these measurements are shown in Table 2.

 Table 2 

Magnitudes of various measured forces in different cells:

 Figure 3 

A schematic depicting two phenomena that can cause retrograde actin flow in vivo, based on [64]. Retrograde flow is postulated to occur either due to release of the molecular clutch and resultant slippage, as seen in Figure a) (where the yellow and green parts of the clutch do not fit), or due to adhesion raking as shown in Figure b) (where the clutch is engaged (yellow and green parts fit) but there is raking of the cytoskeleton against the substrate (blue and white parts)).

As the protruding leading edge adheres to the substrate, the cell also deadheres at the cell body and the rear. This is likely a biochemical process involving the disassembly of the focal adhesions [89-91]. Such a process is mediated by several proteins including the protease calpain, as well as other signals such as Src, FAK and PAK etc. [89-91]. The process of detachment is also influenced by the cytoskeletal contractile forces developed at the rear, and simple mechanics. When adhesions are no longer under the cell, they are under considerable strain, and eventually unbind. On the other hand, if the cell cannot generate sufficient forces to break the adhesions, these adhesion sites become restraints, and prevent the cell from moving forward further. The exact method by which each cell type detaches, however, can differ and depends on the strength and distribution pattern of the attachments and cell speed, and thus is a continued area of research.

In summary, adhesion forces are a critical ingredient of cell movement, mediating the generation of traction forces that allow the protrusion of the leading edge and the translocation of the rest of the cell.

c) Translocation of Cell Body and Rear of the Cell or Retraction Mechanics

The final step of cell movement is translocation of the cell body and the rear of the cell. The retraction force required for this process is generally thought to be generated by the sliding of myosin motors, such as myosin II or Ic, on actin filaments or actin bundles in the cell body and rear. Since the actin filaments and bundles are connected to the cell membrane and the substrate, the force generated can be converted to traction forces that enable the cell to move forward. This idea of contraction of the acto-myosin network as the origin of the retraction force is based on several studies that have explored the role of myosin motors in retraction [92, 94] (note however that contractility does not occur only at the rear and can occur elsewhere, as there is cortical tension around the cell. At the rear, an imbalance of contraction and adhesion causes the rear to be lifted). For example, one experimental study has investigated the role of myosin II motors in retraction by knocking out myosin II in dictyostelium cells [95]. The study demonstrates that, on adhesive surfaces, the myosin minus cells do not retract as well as their normal counterparts do and move more slowly than them. Another study on fish keratocytes shows that the inhibition of myosin contraction causes the cell body to halt, producing a lamellar fragment which continues forward [96]. These studies conclude that conventional myosins play an important role in the movement of the cell body and retraction of the trailing edge [95,96].

Studies on the acto-myosin network also provide estimates for the acto-myosin contractile force; it is similar in magnitude to the polymerization force at the leading edge − on the order of thousands of piconewtons since there are thousands of myosin motors at the rear, each generating ~1 pN of force [38]. Such a myosin generated contractile force is likely to be the primary contributor to the retraction force, but it may not be the only contributor. Other theories for the retraction force include transport mechanisms, which involve the pulling of the cell, with myosin motors, on oriented actin filaments that function as tracks [97]. Another mechanism by which the actin gel in some cell types can create contractile forces is by the process of solation (decrease in gel structure, which could imply disassembly of the network by the severing of filaments or breaking of crosslinks, or unbundling of filaments). A solating actin gel can generate a contractile force of a few piconewtons per actin filament (see calculations in [38,51]).

In order to understand the generation of a contractile force by solation, and to better understand the retraction force in general, recent studies have been performed. Experiments have reconstituted retraction in vitro using crawling nematode sperm cells [98]. These cells offer an ideal system to study crawling, since they are simple prokaryotic cells that use major sperm protein (MSP) to crawl, in a similar process to actin-based eukaryotic cell movement; however, they employ MSP solely to perform the job of cell movement, unlike actin which participates in several other functions of eukaryotic cells [99]. In particular, the study used vesicles – derived from the leading-edge membrane of nematode sperm cells – surrounded by cytoplasm including MSP. The researchers observed that the disassembly or unbundling of MSP bundles (in the presence of Yersinia thyrosine phosphatase (YOP)) attached to the vesicle caused a contraction of individual filaments and led to a contractile force [98]. Thus, they found that retraction forces can be explained by considering cytoskeletal dynamics alone (without considering motors), thereby suggesting an alternate mechanism of generating a contractile force at the rear of the cell. A recent model motivated by this data further elucidates how solely cytoskeletal disassembly generates the necessary force to pull the cell body forward [51]. A qualitative description of the model, which contains two steps, is the following: The first step involves the detachment of filaments from the bundle. A bundle with N filaments, each having a persistence length L_p, has an effective persistence length of N²L_p, and is thus much stiffer than an individual filament [51]. When the filaments detach from the bundle (caused by YOP), its effective persistence length and rigidity (rigidity is directly proportional to L_p) decrease, leading to its contraction due to an increase in entropy. The second step deals with the dissociation of monomers from the filaments (depolymerization). Thus, this kinetic model for disassembly incorporating polymer entropy is able to quantify the retraction forces due to disassembly. However, future experiments are needed to ascertain the relevance and relative contribution (with respect to myosin generated forces, for example) of such a mechanism in generating retraction forces in vivo.

In summary, the retraction force, whose major components are believed to include cytoskeletal disassembly and acto-myosin contraction, is a vital force required to move the bulk of the cell forward and complete the migration cycle.

4. Conclusion

Cell motility is a complex and integrated process that is carefully and precisely orchestrated by the cell with the help of many receptor, crosslinking, bundling, binding, adhesion, motor and other proteins; these proteins serve to determine the direction of cell movement, and to carry out the motility events in an exactly timed manner. The crawling of a cell is a cyclical process driven primarily by actin polymerization and acto-myosin contractility, and can be divided into three parts: protrusion of the leading edge, adhesion of the leading edge and deadhesion at the cell body and rear of the cell, and cytoskeletal contraction to pull the cell body forward as the cell moves.

Although the basic molecular mechanisms of cell movement and the associated signaling pathways are much clearer now than before, there are still a number of open questions regarding the polymerization, adhesion and retraction forces and other mechanisms. For the polymerization force, further experimental studies are required to ascertain the exact role of actin polymerization as the main (active) force mechanism pushing the leading edge. It is likely that in some systems it is not the sole active mechanism pushing the front, similar to the case of the nematode sperm cell, where osmotic pressure is postulated to be the active force mechanism and MSP is a passive generator that fills the space [100]. Hence further investigations are required into which cellular systems actin polymerization and acto-myosin contractility are essential and what their relative contributions are when other force generating mechanisms are present in the same system. If they are the core mechanisms, other questions include determining the role of motor proteins in generating the polymerization force, and testing the force-velocity relations further. As already mentioned, active research areas regarding the adhesion and retraction forces include the exact relation between the force with which the protruding cell edge adheres to the underlying substrate, the retrograde actin flow and cell speed in various cell types, and also the exact origin of the retraction force in vivo.

A thorough understanding of the underlying mechanisms and forces of cell movement is essential for gaining deeper insight into several key biological processes such as morphogenesis, wound healing, neurogenesis and immune response. In addition, cell movement is critical in many diseases including tumor development and metastasis, where cells from a primary tumor move away and spread to other parts of the body. A better understanding of the effective mechanisms by which the cell generates these forces and how these forces operate at the microscopic scale may facilitate incorporating similar principles in engineering various mechanisms at microscopic scales.

Glossary

Adhesion: In physiological environments, cells often adhere to other cells or the extracellular matrix. This is accomplished with the help of adhesion molecules such as integrins, selectins, vinculin, talin and others, which help mediate the interaction between cells and their environment.

(Actin) Polymerization: Actin polymerization is the incorporation of monomers to an actin polymer that results in the elongation of an actin filament. The filament grows preferentially at one end called the plus end. The other end, called the minus end, grows more slowly, with the difference in growth rates between the two ends depending on the actin monomer concentration.

Biopolymer: Biopolymers are polymers found in living organisms and are comprised of repetitive subunits called monomers. Actin, microtubules, intermediate filaments, DNA, RNA, proteins are all biopolymers.

Brownian Motion and the Elastic Brownian Ratchet Model: Brownian motion is the random fluctuation of an object due to thermal energy. It plays a very important role at cellular scales because an object's Brownian fluctuations are inversely proportional to its size. The Elastic Brownian Ratchet Model considers the thermal fluctuation of the cell membrane and the elastic nature of the actin filament in order to explain the force generated by a polymerizing actin filament.

Motor: A motor is anything capable of converting energy into work. In cell motility, myosin is a common molecular motor, which hydrolyzes ATP into ADP, and from this chemical energy does mechanical work on an actin filament.

Navier-Stokes Equations: These are partial differential equations and the fundamental equations that describe the flow of fluids. The equations are derived by considering all the forces acting on a fluid particle at any time, which include viscous forces in the fluid as well as pressure changes inside the fluid.

Polymerization Force: The force generated by actin filaments growing at the leading edge and pushing against the cell membrane.

Protrusion Force: The force developed at the leading edge of the cell for lamellipodial movement.

Relation Among Forces: Stalling the cell in various ways gives estimates of the forces generated by the cell body, lamellipodium etc. If the entire cell/cell body translocation is stalled, this gives an estimate of the traction force, while stalling the lamellipodial protrusion gives the lamellipodial protrusive force. Note again that the traction forces applied by the cell to the substrate are caused by the (largely myosin generated) contractile forces, but are not equal to them, as the contractile forces are not necessarily at their maximum in the direction of motion. Also, as explained using the molecular clutch hypothesis, the transduction from contraction to traction is mediated by several factors, such as the adhesion mechanics, as well as the cell's elastic and viscous properties. Similarly, the amount of polymerization force that is converted and used for protrusion (the rest contributes to retrograde flow) also depends on the state of the “molecular clutch”.

Retrograde Flow: Retrograde flow is the movement of actin with respect to the substrate towards the center of the cell i.e. in the opposite direction of cell motion and with a velocity that is generally different than the forward protrusion velocity. Increased retrograde flow in a cell generally results in a reduction of speed, while a decreased retrograde flow generally results in an increase in speed, as the overall actin flow mechanics is seen to run at a constant speed.

Stall Force: The force required to stall the forward translocation of the cell body (whole cell stall force) or block the protrusion of the lamellipodium (which is the lamellipodial stall force/ local stall force).

Traction Force: The force exerted by a moving cell on the substrate as the bulk of the cell (cell body/nucleus etc.) translocates. In other words, it is the force the cell generates against the substrate in order to move forward, given its adhesion to the substrate. Local traction forces can be quite large, but the net traction force may be much smaller, as the majority of the forces are contractile and cancel out in vector summation.

Acknowledgements

Revathi acknowledges many discussions and support from her post-doctoral advisor Alex Mogilner. We also acknowledge discussions with T. Oliver, G. Civelekoglu-Scholey, and valuable help from D. Martin, I. Brust-Mascher and D. Cheerambathur for a critical perusal of this manuscript and several useful suggestions.

Conflict of interest

The authors have declared that no conflict of interest exists.

References

1. Alberts B, Johnson A, Lewis J. et al. Molecular Biology of the Cell, 4e. Garland Science. 2002

2. Dogterom M, Yurke B. Measurement of the force-velocity relation for growing microtubules. Science. 1997;278(5339):856-60

3. Block SM, Asbury CL, Shaevitz JW. et al. Probing the kinesin reaction cycle with a 2D optical force clamp. Proc Natl Acad Sci USA. 2003;100:2351-2356

4. Finer TJ, Simmons RM, Spudich JA. Single myosin molecule mechanics: piconewton forces and nanometre steps. Nature. 1994;368:113-119

5. Parekh SH, Chaudhuri O, Theriot JA. et al. Loading history determines the velocity of actin-network growth. Nat Cell Biol. 2005;7(12):1219-23

6. Theriot JA. The polymerization motor. Traffic. 2000;1:19-28

7. Brunner CA, Ehrlicher A, Kohlstrunk B. et al. Cell migration through small gaps. Eur Biophys J. 2006;35(8):713-9

8. Oliver T, Dembo M, Jacobson K. Traction forces in locomoting cells. Cell Motil Cytoskeleton. 1995;31(3):225-40

9. Kaverina I, Krylyshkina O, Small JV. Regulation of substrate adhesion dynamics during cell motility. Int J Biochem Cell Biol. 2002;34(7):746-61

10. Morse D. Viscoelasticity of concentrated isotropic solutions of semi-flexible polymers. 1. model and stress tensor; 2. linear response. Macromolecules. 1998;31:7030-7044

11. Gittes F, Mickey B, Nettleton J. et al. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J Cell Biol. 1993;120(4):923-34

12. Lodish H, Berk A, Zipursky SL. et al. Molecular Cell Biology, 4e. WHFreeman and Company. 2000

13. Pampaloni F, Lattanzi G, Jonas A. et al. Thermal fluctuations of grafted microtubules provide evidence of a length-dependent persistence length. Proc Natl Acad Sci USA. 2006;103(27):10248-53

14. Dogterom M, Kerssemakers JW, Romet-Lemonne G. et al. Force generation by dynamic microtubules. Curr Opin Cell Biol. 2005;17(1):67-74

15. Zackroff RV, Goldman RD. In vitro assembly of intermediate filaments from baby hamster kidney (BHK-21) cells. Proc Natl Acad Sci USA. 1979;76(12):6226-6230

16. Betz T, Lim D, Kas JA. Neuronal growth: a bistable stochastic process. Phys Rev Lett. 2006;96(9):098103

17. Hofman P, d'Andrea L, Guzman E. et al. Neutrophil F-actin and myosin but not microtubules functionally regulate transepithelial migration induced by interleukin 8 across a cultured intestinal epithelial monolayer. Eur Cytokine Netw. 1999;10(2):227-36

18. Pollard TD, Blanchoin L, Mullins RD. Molecular mechanisms controlling actin filament dynamics in nonmuscle cells. Annu Rev Biophys Biomol Struct. 2000;29:545-76

19. Pollard TD, Borisy G. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 2003;112(4):453-465

20. Zheng JQ, Wan JJ, Poo MM. Essential role of filopodia in chemotropic turning of nerve growth cone induced by a glutamate gradient. J Neurosci. 1996;16(3):1140-9

21. Vignjevic D, Kojima S, Aratyn Y. et al. Role of fascin in filopodial protrusion. J Cell Biol. 2006;174(6):863-75

22. Euteneuer U, Schliwa M. The Function of Microtubules in Directional Cell Movement. Annals of the New York Academy of Sciences. 1986;466(1):867-886

23. Helfand BT, Chang L, Goldman RD. Intermediate filaments are dynamic and motile elements of cellular architecture. J Cell Sci. 2004;117(Pt 2):133-41

24. Parent C, Devreotes P. A Cell's Sense of Direction. Science. 1999;284:765-770

25. Abercrombie M. The Croonian Lecture, 1978: The Crawling Movement of Metazoan Cells. Proc Roy Soc Lond B. 1980;207:129-147

26. Fukui Y. Mechanistics of amoeboid locomotion: signal to forces. Cell Biol Int. 2002;26(11):933-44

27. Humphrey D, Duggan C, Saha D. et al. Active fluidization of polymer networks through molecular motors. Nature. 2002;416(6879):413-6

28. Maly IV, Borisy GG. Self-organization of a propulsive actin network as an evolutionary process. Proc Natl Acad Sci USA. 2001;98(20):11324-9

29. Rafelski SM, Theriot JA. Crawling toward a unified model of cell mobility: spatial and temporal regulation of actin dynamics. Annu Rev Biochem. 2004;73:209-39

30. Fletcher DA, Theriot JA. An introduction to cell motility for the physical scientist. Phys Biol. 2004;1(1-2):T1-10

31. Mogilner A. On the edge: modeling protrusion. Curr Opin Cell Biol. 2006;18(1):32-9

32. Li S, Guan JL, Chien S. Biochemistry and biomechanics of cell motility. Annu Rev Biomed Eng. 2005;7:105-50

33. Carlier MF, Le Clainche C, Wiesner S. et al. Actin-based motility: from molecules to movement. Bioessays. 2003;25(4):336-45

34. Mogilner A, Oster G. Cell motility driven by actin polymerization. Biophys. J. 1996;71:3030-3045

35. Mogilner A, Oster G. Force generation by actin polymerization II: the elastic ratchet and tethered filaments. Biophys. J. 2003;84:1591-1605

36. Carlsson AE. Growth velocities of branched actin networks. Biophys J. 2003;84(5):2907-18

37. Carlsson AE. Growth of branched actin networks against obstacles. Biophys J. 2001;81(4):1907-23

38. Mogilner A, Oster G. Polymer motors: pushing out the front and pulling up the back. Curr Biol. 2003;13(18):R721-33

39. Dickinson RB, Caro L, Purich DL. Force generation by cytoskeletal filament end-tracking proteins. Biophys J. 2004;87(4):2838-54

40. Upadhyaya A, van Oudenaarden A. Biomimetic systems for studying actin-based motility. Curr Biol. 2003;13(18):R734-44

41. McGrath JL, Eungdamrong NJ, Fisher CI. et al. The force-velocity relationship for the actin-based motility of Listeria monocytogenes. Curr Biol. 2003;13(4):329-32

42. Wiesner S, Helfer E, Didry D. et al. A biomimetic motility assay provides insight into the mechanism of actin-based motility. J Cell Biol. 2003;160(3):387-98

43. Pantaloni D, Le Clainche C, Carlier MF. Mechanism of actin-based motility. Science. 2001;292(5521):1502-6

44. van der Gucht J, Paluch E, Plastino J. et al. Stress release drives symmetry breaking for actin-based movement. Proc Natl Acad Sci USA. 2005;102(22):7847-52

45. Schwartz IM, Ehrenberg M, Bindschadler M. et al. The role of substrate curvature in actin-based pushing forces. Curr Biol. 2004;14(12):1094-8

46. Bernheim-Groswasser A, Wiesner S, Golsteyn RM. et al. The dynamics of actin-based motility depend on surface parameters. Nature. 2002;417(6886):308-11

47. Noireaux V, Golsteyn RM, Friederich E. et al. Growing an actin gel on spherical surfaces. Biophys J. 2000;78(3):1643-54

48. Marcy Y, Prost J, Carlier MF. et al. Forces generated during actin-based propulsion: a direct measurement by micromanipulation. Proc Natl Acad Sci USA. 2004;101(16):5992-7

49. Upadhyaya A, Chabot JR, Andreeva A. et al. Probing polymerization forces by using actin-propelled lipid vesicles. Proc Natl Acad Sci USA. 2003;100(8):4521-6

50. Giardini PA, Fletcher DA, Theriot JA. Compression forces generated by actin comet tails on lipid vesicles. Proc Natl Acad Sci USA. 2003;100(11):6493-8

51. Wolgemuth CW, Miao L, Vanderlinde O. et al. MSP dynamics drives nematode sperm locomotion. Biophys J. 2005;88(4):2462-71

52. Thoumine O, Kocian P, Kottelat A. et al. Short-term binding of fibroblasts to fibronectin: optical tweezers experiments and probabilistic analysis. Eur. Biophys. J. 2000;29(6):398-408

53. Atilgan E, Wirtz D, Sun SX. Mechanics and dynamics of actin-driven thin membrane protrusions. Biophys J. 2006;90(1):65-76

54. Mogilner A, Edelstein-Keshet L. Regulation of actin dynamics in rapidly moving cells: a quantitative analysis. Biophys J. 2002;83(3):1237-58

55. Raucher D, Sheetz MP. Cell spreading and lamellipodial extension rate is regulated by membrane tension. J Cell Biol. 2000;148(1):127-36

56. Karl I, Bereiter-Hahn J. Tension modulates cell surface motility: A scanning acoustic microscopy study. Cell Motil Cytoskeleton. 1999;43(4):349-59

57. Lee J, Leonard M, Oliver T. et al. Traction forces generated by locomoting keratocytes. J Cell Biol. 1994;127(6 Pt 2):1957-64

58. Munevar S, Wang Y, Dembo M. Traction force microscopy of migrating normal and H-ras transformed 3T3 fibroblasts. Biophys J. 2001;80(4):1744-57

59. Suter DM, Forscher P. Substrate-cytoskeletal coupling as a mechanism for the regulation of growth cone motility and guidance. J. Neurobiol. 2000;44:97-113

60. Medeiros NA, Burnette DT, Forscher P. Myosin II functions in actin-bundle turnover in neuronal growth cones. Nat Cell Biol. 2006;8(3):215-26

61. Jay DG. The clutch hypothesis revisited: ascribing the roles of actin-associated proteins in filopodial protrusion in the nerve growth cone. J Neurobiol. 2000;44(2):114-25

62. Lin CH, Espreafico EM, Mooseker MS. et al. Myosin drives retrograde F-actin flow in neuronal growth cones. Neuron. 1996;16(4):769-82

63. Lin CH, Forscher P. Growth cone advance is inversely proportional to retrograde F-actin flow. Neuron. 1995;14(4):763-71

64. Jurado C, Haserick JR, Lee J. Slipping or gripping? Fluorescent speckle microscopy in fish keratocytes reveals two different mechanisms for generating a retrograde flow of actin. Mol Biol Cell. 2005;16(2):507-18

65. Watanabe N, Mitchison TJ. Single-molecule speckle analysis of actin filament turnover in lamellipodia. Science. 2002;295(5557):1083-6

66. Fukui Y, Kitanishi-Yumura T, Yumura S. Myosin II-independent F-actin flow contributes to cell locomotion in dictyostelium. J Cell Sci. 1999;112( Pt 6):877-86

67. Vallotton P, Danuser G, Bohnet S. et al. Tracking retrograde flow in keratocytes: news from the front. Mol Biol Cell. 2005;16(3):1223-31

68. Brown ME, Bridgman PC. Retrograde flow rate is increased in growth cones from myosin IIB knockout mice. J Cell Sci. 2003;116(Pt 6):1087-94

69. Diefenbach TJ, Latham VM, Yimlamai D. et al. Myosin 1c and myosin IIB serve opposing roles in lamellipodial dynamics of the neuronal growth cone. J Cell Biol. 2002;158(7):1207-17

70. Wang FS, Liu CW, Diefenbach TJ. et al. Modeling the role of myosin 1c in neuronal growth cone turning. Biophys J. 2003;85(5):3319-28

71. Cai Y, Biais N, Giannone G. et al. Nonmuscle myosin IIA-dependent force inhibits cell spreading and drives F-actin flow. Biophys J. 2006;91(10):3907-20

72. Henson JH, Svitkina TM, Burns AR. et al. Two components of actin-based retrograde flow in sea urchin coelomocytes. Mol Biol Cell. 1999;10(12):4075-90

73. Mitchison T, Kirschner M. Cytoskeletal dynamics and nerve growth. Neuron. 1988;1(9):761-72

74. Zaman MH, Kamm RD, Matsudaira P. et al. Computational model for cell migration in three-dimensional matrices. Biophys J. 2005;89(2):1389-97

75. Gupton SL, Waterman-Storer CM. Spatiotemporal feedback between actomyosin and focal-adhesion systems optimizes rapid cell migration. Cell. 2006;125(7):1361-74

76. Shreiber DI, Barocas VH, Tranquillo RT. Temporal variations in cell migration and traction during fibroblast-mediated gel compaction. Biophys J. 2003;84(6):4102-14

77. Kruse K, Joanny JF, Julicher F. et al. Contractility and retrograde flow in lamellipodium motion. Phys Biol. 2006;3(2):130-7

78. Tan J, Shen H, Saltzman WM. Micron-scale positioning of features influences the rate of polymorphonuclear leukocyte migration. Biophys J. 2001;81(5):2569-79

79. Ponti A, Vallotton P, Salmon WC. et al. Computational analysis of F-actin turnover in cortical actin meshworks using fluorescent speckle microscopy. Biophys J. 2003;84(5):3336-52

80. Geiger B, Bershadsky A, Pankov R. et al. Transmembrane crosstalk between the extracellular matrix--cytoskeleton crosstalk. Nat Rev Mol Cell Biol. 2001;2(11):793-805

81. Bohnet S, Ananthakrishnan R, Mogilner A. et al. Weak force stalls protrusion at the leading edge of the lamellipodium. Biophys J. 2006;90:1810-1820

82. Prass M, Jacobson K, Mogilner A. et al. Direct measurement of the lamellipodial protrusive force in a migrating cell. J Cell Biol. 2006;174(6):767-72

83. Wang JH, Lin JS. Cell traction force and measurement methods. Biomech Model Mechanobiol. 2007 [Epub ahead of print]

84. Munevar S, Wang YL, Dembo M. Distinct roles of frontal and rear cell-substrate adhesions in fibroblast migration. Mol Biol Cell. 2001;12(12):3947-54

85. Dembo M, Wang YL. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys J. 1999;76(4):2307-16

86. Galbraith CG, Sheetz MP. A micromachined device provides a new bend on fibroblast traction forces. Proc Natl Acad Sci USA. 1997;94(17):9114-8

87. Curtis AS, Sokolikova-Csaderova L, Aitchison G. Measuring cell forces by a photoelastic method. Biophys J. 2006 [Epub ahead of print]

88. Oliver T, Dembo M, Jacobson K. Separation of propulsive and adhesive traction stresses in locomoting keratocytes. J Cell Biol. 1999;145(3):589-604

89. Ridley AJ, Schwartz MA, Burridge K. et al. Cell migration: integrating signals from front to back. Science. 2003;302(5651):1704-9

90. Ridley AJ. Rho GTPases and cell migration. J Cell Sci. 2001;114(Pt 15):2713-22

91. Ridley AJ. Rho family proteins: coordinating cell responses. Trends Cell Biol. 2001;11(12):471-7

92. Svitkina TM, Verkovsky AB, McQuade KM. et al. Analysis of the actin-myosin II system in fish epidermal keratocytes: Mechanism of cell body translocation. J Cell Biol. 1997;139:397-415

93. Eddy RJ, Pierini LM, Matsumura F. et al. Ca2+-dependent myosin II activation is required for uropod retraction during neutrophil migration. J Cell Sci. 2000;113:1287-1298

94. Kolega J, Taylor DL. Gradients in the concentration and assembly of myosin II in living fibroblasts during locomotion and fiber transport. Mol Biol Cell. 1993;4:819-836

95. Jay PY, Pham PA, Wong SA. et al. A mechanical function of myosin II in cell motility. J Cell Sci. 1995;108( Pt 1):387-93

96. Verkhovsky AB, Svitkina TM, Borisy GG. Self-polarization and directional motility of cytoplasm. Curr Biol. 1999;9(1):11-20

97. Mitchison TJ, Cramer LP. Actin-based cell motility and cell locomotion. Cell. 1996;84:371-79

98. Miao L, Vanderlinde O, Stewart M. et al. Retraction in amoeboid cell motility powered by cytoskeletal dynamics. Science. 2003;302(5649):1405-7

99. Roberts TM, Stewart M. Acting Like Actin: The Dynamics of the Nematode Major Sperm Protein (MSP) Cytoskeleton Indicate a Push-Pull Mechanism for Amoeboid Cell Motility. J Cell Biol. 2000;149:7-12

100. Joanny JF, Julicher F, Prost J. Motion of an adhesive gel in a swelling gradient: a mechanism for cell locomotion. Phys Rev Lett. 2003;90(16):168102

Author contact

Correspondence to: Dr. Revathi Ananthakrishnan, email: revathiedu

Footnotes

Received 2007-1-21
Accepted 2007-5-27
Published 2007-6-1

Citation styles

©2024 Ivyspring International Publisher. Terms of use