Impact Factor
ISSN: 1449-2288
Int J Biol Sci 2009; 5(2):161-170. doi:10.7150/ijbs.5.161 This issue Cite
Review
Understanding Quantitative Genetics in the Systems Biology Era
Key Laboratory of Agricultural Animal Genetics, Breeding and Reproduction of Ministry of Education, Huazhong Agricultural University, Wuhan 430070, P. R. China
Received 2008-12-3; Accepted 2009-1-21; Published 2009-1-27
Abstract
Biology is now entering the new era of systems biology and exerting a growing influence on the future development of various disciplines within life sciences. In early classical and molecular periods of Biology, the theoretical frames of classical and molecular quantitative genetics have been systematically established, respectively. With the new advent of systems biology, there is occurring a paradigm shift in the field of quantitative genetics. Where and how the quantitative genetics would develop after having undergone its classical and molecular periods? This is a difficult question to answer exactly. In this perspective article, the major effort was made to discuss the possible development of quantitative genetics in the systems biology era, and for which there is a high potentiality to develop towards "systems quantitative genetics". In our opinion, the systems quantitative genetics can be defined as a new discipline to address the generalized genetic laws of bioalleles controlling the heritable phenotypes of complex traits following a new dynamic network model. Other issues from quantitative genetic perspective relating to the genetical genomics, the updates of network model, and the future research prospects were also discussed.
Keywords: systems quantitative genetics, definition, dynamic network model, prospect
1. Introduction
There is a trend in life sciences development that, as a discipline, the development of Biology depends on accumulating and assimilating the new knowledge in other various disciplines within life sciences, and in reverse, provides a common time division of their historical stages. From Classical Biology to Molecular Biology, various life sciences have been led into the molecular era, e.g., the emergences of the molecular biology-related disciplines such as molecular nutriology, molecular immunology, molecular ecology, molecular evolution and phylogenetics. Now, the time has come for Biology to enter the era of systems biology after having undergone its classical and molecular periods [1-3], which is exerting an increasing influence on the transformation of life sciences from a reductionist to a systemic paradigm. It is believed that the advent of systems biology would inevitably give explosive birth to a diversity of new fields being dressed up with a "systems" prefix as the "molecular" in the molecular era.
Quantitative genetics was founded, in evolutionary terms, by the originators of the modern synthesis. This field is a relatively independent branch of life sciences but the one increasingly applied in a wide spectrum of scientific disciplines such as evolution, animal and plant breeding, behavioral genetics, conservation biology, medical genetics, ecology, anthropology and psychology [4-11], which particularly has played a crucial role in relieving the worldwide famine through genetic improvement of the productivity of the agricultural animals and crops. It is anticipated that new development in quantitative genetics will be of great benefit to various other branches of life sciences. An outline of near 100 years' published literatures in this field had documented that the historical development of quantitative genetics was rough running after that of Biology. In its history, the quantitative genetics had gone through the first and second developmental stages, i.e., the classical and molecular quantitative genetics, respectively [12] [13], which, in despite of having partial overlap, were as expected corresponding to the classical and molecular periods of Biology. It could be concluded that Biology has also provided the discipline background for the development of quantitative genetics. After the long development from classical to molecular quantitative genetics, it might be timely for quantitative genetics to be brought into the third developmental stage in the coming era of systems biology.
2. Proposal of systems quantitative genetics
2.1 Background and definition
Our knowledge of the classical and molecular quantitative genetics has undergone a striking expansion in the last century. The classical quantitative genetics considers a black box to reveal the holistic status of all genes associated with the variation of investigated traits by complicated statistical methods [14]. The subsequently (but partially overlapped in time) established molecular quantitative genetics mainly focuses on evaluating the coupling association of the polymorphic DNA sites with the phenotypic variations of quantitative and complex traits, as well as dissecting their genetic architectures, but which never pays attention to the details of how genetic information is transcriptionally and translationally processed. The absence of the inside functional information prevents a definitive identification of the gene(s) underlying the control of target traits, which usually requires a subsequent validation of the gene function in more future generations of the same population or other different populations, or quantitative complementation test. In living organisms, there are complex genetic and epigenetic mechanisms to the molecular regulation of the phenotypic characteristics of a trait at multiple levels, including DNA sequence variation, pre- and post- transcription events, pre- and post-translation processings, and the hierarchical or global gene network. It is now well known that, from DNA to phenotype, the deletion, addition, substitution, covalent modification, alternative packaging of nucleotides, alternative splicing of mRNAs, and even other kinds of soft inheritance regulations widely participate in the process of handling genetic information [15]. Involving in both hard and soft inheritance, the genetic information flow from DNA polymorphisms to phenotypic variations is not linearly dispersed in living organisms. This determines that there is no complete congruence between DNA and phenotype. It is very necessary to open the black box between genes and phenotypes.
In fact, the phenomena that heritable component of phenotypic variation was aroused without DNA sequence changes have been proven to have a frequent occurrence at both cellular and organism levels [16-18], which reveal that the variome at the DNA level cannot provide a full elucidation of the heritable phenotypes. As suggested by Johannes et al. (2008), more effort should be given to capture the potentially dynamic interplay between chromatin and DNA sequence factors in complex traits [19]. There are also many evidences, more accumulated in plants, that non-Mendelian genetic factors modifying the DNA can be inherited. On many occasions, quantitative genetic investigations of target traits only from DNA polymorphisms is no longer absolutely appropriate, though it is still debated how important the non-DNA sequence variation is in controlling the inheritance of phenotypes. Up to date, some pilot work to address this subject has already been undertaken, in which the molecular information mediated between DNA and phenotype such as RNA splicing, proteins, metabolites or their combinations has been brought into the new research area of quantitative genetics [20-23]. How to weigh and integrate the contribution of biological molecules at different levels and their interactions to the heritable component of phenotypes is a new exciting challenge brought to us, of which both classical and molecular quantitative genetics are incapable.
Further development of quantitative genetics based on the systems biology thinking would provide an alternative solution to this challenge. Now it is perhaps timely for quantitative genetics to enter into its third developmental stage. Here, as coined by us previously [24], we propose to use the term "Systems Quantitative Genetics" as the general name of the third generation of quantitative genetics. Aylor and Zeng (2008) have also introduced the concept of systems biology into quantitative genetics, in which a framework was proposed to estimate and interpret epistasis [25], but it involved the gene expression traits rather than the macroscopic phenotype of biomedically, economically, or evolutionarily important traits. In our opinion, the systems quantitative genetics is an interdisciplinary marriage of quantitative genetics and systems biology. Historically inherited from the classical and molecular quantitative genetics, the systems quantitative genetics, following a new dynamic network model, could be defined as a new discipline that addresses the generalized genetic laws of bioalleles (e.g., DNA sequence alleles, epialleles [19], transcriptalleles, protealleles, metaboalleles and physialleles) underlying the phenotypic variations of interesting traits based on the new thoughts of systems biology, which is beyond the scope of molecular quantitative genetics and mainly focuses on parsing the ab initio mechanism underpinning the relationship between the phenotypes and the analytic status (dynamic network rather than black box or a few major genes) of genes in investigated traits.. There are distinct differences among three generations of quantitative genetics (Table 1).
Comparisons among classical, molecular and systems quantitative genetics
| Comparative items | Classical quantitative genetics | Molecular quantitative genetics | Systems quantitative genetics |
|---|---|---|---|
| Discipline background | Classical biology | Molecular biology | Systems biology |
| Depiction of genic system | Holistic status of all genes | Analytical status of major gene and holistic status of minor genes | Analytical status of a large set of genes (and downstream molecules) |
| Statistical property | Implicit consideration for all genes | Partially explicit consideration for major gene and implicit consideration for minor genes | Fully explicit consideration for a large set of genes (and downstream molecules) |
| Phenotypic property | Static holistication of phenotype | Static decomposition of phenotype | Dynamic decomposition of phenotype |
| Variation sources to phenotype | DNA sequence alleles | DNA sequence alleles and infrequent epialleles | Bioalleles of molecules at multiple levels |
| Model assumption | Polygenic model | Major gene plus polygene mixed inheritance model | Gene network model |
| Genetic laws involved | Mendelian laws | Mendelian laws and partial non-Mendelian laws | generalized genetic laws involving in both Mendelian and non-Mendelian laws |
2.2. Beyond the genetical genomics
Genetical genomics, also colloquially referred to as "expression genetics", was first introduced by Janson and Nap [26], and the initial purpose of which was to provide a powerful paradigm for mapping gene expression quantitative trait loci (eQTL) at a global level [27] [28]. The genetical genomics or eQTL is technically a marriage of high-throughput expression profiling technology and quantitative trait loci (QTL) analysis, but which still holds the underlying statistical principles of QTL mapping. The body of knowledge of this field is growing at an extraordinary fast rate. It appears that the genetical genomics is now leading the frontier research of quantitative genetics [29]. Nevertheless, both expressed structural genes and eQTLs simultaneously belong to the category of gene per se, which is quite different from the conventional relationship between QTL and the real phenotype in traditional linkage analysis. Such difference results in that the specific regulatory relationships between causal loci and the structural genes could be respectively described by two types of eQTLs: cis- and trans-eQTL [30] [31]. Actually, the main aim of genetical genomics is now providing the use for massively revealing the genetic determinant of the expression abundance as well as the derivative characters such as the stability of transcript, the timing of transcription, the alternative splicing [32-35], and the reconstruction of gene regulatory network [36] [37] in various species.
From gene expression data to whole-organism traits, there is an unsolved paradox for genetical genomics (Section 2.2.1). In current, the genetical genomics seems incapable to identify the as-yet-undiscovered genes underlying the macroscopic phenotypic characteristics and evolutionary outcomes without other ancillary evidences [38] [39], though in which the "so-called" phenotype -- transcript abundance of investigated gene is treated as a highly heritable quantitative trait. Entirely unlike this, the goal of systems quantitative genetics is to unravel the ab initio mechanism of the multilevel molecules underlying the heritable phenotypic variations, rather than the mRNA abundance, of organismal traits. There is obvious difference in essence between these two fields. The genetical genomics would therefore not expected to belong to the category of systems quantitative genetics due to its only concern at the transcriptional level. A more suitable orientation of the genetical genomics in its current status is an extending application of molecular quantitative genetics in which the issues of functional genomics, e.g., massive identification of unknown cis regulatory elements and transcription factors, genetic determinants of metabolites, and reconstruction of genetic regulatory network, are addressed by the well-established approaches or extension methods of molecular quantitative genetics. The principles and techniques of genetical genomics still fall within the category of the second generation quantitative genetics, though, of which the algorithms for high dimensional data potentially provides a valuable contribution to the development of systems quantitative genetics. In our opinion, as a new discipline, the multilevel-focusing systems quantitative genetics is far beyond what the genetical genomics could hold.
2.2.1. Paradox encountered by genetical genomics
There have been some researches taking efforts to identify the undiscovered genes controlling the organismal traits at tissular, organic, systemic and the entire organism levels by means of gene expression data [21] [40-44]. However, these researches were performed under the precondition that either the genes with prior biological functions are involved in the measurements, or the gene expression measurements are done in specific tissues or cell types with a certain biological relevance to target phenotypes [45]. Due to the direct or indirect reliance on the prior knowledge of the expressed genes, to a certain extent, these investigations led themselves into a circular argument at the philosophic level. Up to date, it is hard to directly confirm that the loci controlling the expression variation of function-unknown genes also control the phenotypic variation of macroscopic traits. For the function-known genes, the genetical genomics just provides a validation rather than an ab initio mechanistic explanation, and seems to argue in a circle for the purpose of gene discovery. On the other hand, for the function-unknown genes, it presents linkages between the polymorphic sites and the mRNA expression traits of function-unknown genes, which, without other information, remains unsure whether the polymorphic sites or the expressed genes are directly associated with the macroscopic phenotypes of interesting traits. There seems a paradox for genetical genomics to conduct the ab-initio mechanistic studies that systems quantitative genetics is concerned with.
3. From polygenic model to gene network model
3.1. Historical heritage of quantitative trait gene model
There have hitherto been proposed two quantitative trait gene (QTG) models to describe the biological archetype of genes underlying quantitative traits: the polygenic model and the major gene plus polygene mixed inheritance model (shortened as mixed model below). From a scientific logic perspective, the QTG model provides a basis for the theory development of quantitative genetics. Most or almost all of the existed mathematical modelings of quantitative trait genes were conceptually developed through extending or transforming the two basic biological models. The former supplies the base for the theorization of classical quantitative genetics [12] [46] [47]. The latter also forms the theoretical basis of molecular quantitative genetics because for which the existence of major genes or QTLs is a precondition to the molecular quantitative genetic analyses [48-51]. It could be generalized that the base of quantitative genetics theories logically relies on the hypothesized archetype of quantitative trait genes, though the formal depictions of the polygenic and mixed models were not strictly prior to the shape of some concrete theories in the developmental history of quantitative genetics.
The polygenic model takes the whole of the genes governing target trait(s) as a black box, and of which the holistic properties were roughly depicted with several simplifying assumptions [12] [52] [53]. Consequently, with more understanding of the biological nature of quantitative trait gene, the empirical depictions of polygenic model were no longer compatible with the known biological reality. It had been aware that the effect sizes of genes (loci) controlling quantitative traits are not entirely equal, but usually a few major genes and many minor genes are involved in most cases. On many occasions, there were large-effect genes (loci) that could be statistically detected [54] [55]. With introduction of application of molecular biology into quantitative genetics, the mixed model had gradually taken shape to modify the empirical assumptions of polygenic model in practice (Table 2), which, in a simple consideration, was realized by adding major gene(s) to the polygenic model. The mixed model made the portrait of quantitative trait gene was no longer a black box to us, and based on which we can individuate the large-effect genes from the polygenic sets. And, theoretically but not exactly going after the formal formulation of the mixed model in time order, the subsequent the birth and prosperity of molecular quantitative genetics has much benefited from such update. However, with time going on, the mechanistic intuition and an increasingly large volume of knowledge of life sciences contradict the assumptions of mixed model as well. It is now very clear that the characteristics of quantitative traits are usually the consequence of the structure of genetic regulatory networks and the parameters that control the dynamics of those networks [56]. Although paying attention to the difference of gene effect sizes, the hierarchical rank of genes in mixed model is not determined as in polygenic model, which essentially exhibits a parallel rather than hierarchical or network relationship of quantitative trait genes. It does not reflect the fact. Obviously, in current framework, the assumptions of mixed model also lack an interpretable biological reality and are empirical in nature. It is clear that both polygenic and mixed models just provide a pseudo- or quasi-archetype of quantitative trait gene.
Main points of mixed model updated from polygenic model
| Polygenic model | Mixed model a |
|---|---|
| All variable genes have two possible alleles | Many variable genes have more than two alleles in fact |
| Each contributing gene has small and relatively equal effects | Effect size of each contributing gene is not entirely equal; there are both major and minor genes [57] |
| The allele effects of each gene are only additive | Besides additive, the allele effects of certain genes are also non-additive on some occasions [58] |
| There is no dominance on each locus | There are (over-, co-, partial or incomplete) dominance loci [59] [60] |
| There is no epistasis or interaction among different loci contributing to the target trait | There often is epistasis or complex interaction among different loci contributing to the target trait [25] [61] [62] |
| The genes are segregating independently | There are linkages between loci [63-65] |
| Target trait depends solely on genetics, and environmental influences can be ignored | The merit of target trait depends on genetic and environmental factors and their interactions [66] [67] |
| a So far, there has been a lack of a one-time thorough depiction of mixed model. The updates of the mixed model from polygenic one have been gradually solved by separate and fragmentary investigations. | |
3.2. Gene network model: novel modification
With the biological unreality of the earlier two QTG models being recognized, it needs an updated model or completely new one to adapt the coming development of systems quantitative genetics. Here, according to the viewpoint of systems biology and the real biological features of quantitative trait genes, we propose a Gene Network Model (hereafter referred to as network model) to update the QTG model (Section 3.2.1).
Unlike the gene regulatory network in functional genomics [68] [69], the priority goal of network model is to exploit the disturbance principle of gene network under the condition of varying input of both inside and outside factors, as well as the across-generational robustness properties of network output, in which investigation of variation of network output is far beyond reconstruction of network architecture. In order to achieve the above purpose, the output-constrained elements on the nodes, hubs or modules of quantitative genetic network should be treated as analytical objects rather than particles, e.g., explicit equations or nested functions for formulating the mutation inside a causal gene. In theory, such treatment ensures that the event that the mutation within a causal gene affects the within- and across-generation behaviors of the gene network is of predictability and controllability, though there currently still are great challenges and difficulties in the mathematical solutions. Although the contents of the network model developed by us might be partially or mainly controversial, we think, a broad consensus would take a considerable time, certainly not less than the time that the mixed model have ever taken.
3.2.1. Updated contents of the dynamic network model
- Genes underlying the phenotypic variations of quantitative and complex traits agree with a hierarchical/network relationship, which is deciphered by the four-dimensionalization or dynamic tridimensionalization of biological molecules (e.g., genes, noncoding RNAs, proteins, metabolites and signaling components) via integrating the interactions of multiple components from the data provided by genome-wide mutagenesis libraries, in vivo transcriptional and epigenetic profiles and other biological molecules profiles during ontogenesis or trait development;
- To assess the interindividual and intergroup variability, the network of quantitative trait genes in different individuals from the same species is topologically homeomorphic at the four-dimensional level, which means that the network topology is four-dimensionally species-specific and evolutionarily stable;
- Within- and across-generational transfer of network variation follows both Mendelian and non-Mendelian inheritance rules;
- Phenotypic scales of target traits can be considered as the accumulated output of the network until the measurement time;
- Phenotypic variation of quantitative trait can be described as the disturbance of four-dimensional network induced by the bioalleles of generalized genetic factors and their interactions. Systems quantitative genetic analyses of target traits can be theoretically realized through the measurements of network parameters;
- To provide reasonable predictability and controllability for the complete genetic architectures of target traits, the components on the output-constrained nodes or hubs of the gene network are not particles but "Information Boxes";
- Disturbance factors affect the phenotypes of target traits completely depending on the network characteristics. Under a certain network, the effects of both hard and soft inheritance factors on target traits are of predictability and controllability.
3.3. Compatibility between mixed and network models
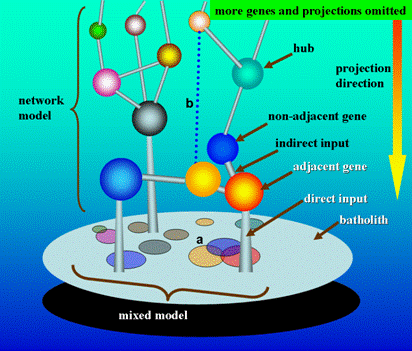
It is certain that the polygenic and mixed models are logistically compatible. There is also a necessity to assess whether or not it is compatible between the mixed and network models. It can be seen from Figure 1 that a network model could yield a mixed model through dimension-reducing mapping, which means that the mixed model is just a special case of the network model under the condition of dimension-reducing simplification. In contrast to the depictions of mixed model, the network model is more in accordance with the biological reality, and has a better ability to predict the genetic architectures of target traits. Obviously, the network model could be downwards compatible with the old mixed model, which indicates the network model is a more reasonable and profound model, and can replace the old one.
Simplified theoretical machinery of quantitative genetics under network model. In this simple scenario, the tridimensional architecture of genes denotes the network model and the projection image of genes on the surface of the batholith denotes the mixed model. It is easy to understand that the mixed model is just a dimension reduction mapping of the network model. As hypothesized in Section 3.2.1, the phenotypic measurement equalizes the accumulated output of gene network, and thus here the batholith supportive of the gene network can be abstractively expressed as the phenotype. Considering a tridimensional relationship in the network model, the batholith only receives the direct input information of adjacent genes, but indirectly the non-adjacent genes act, which means the effects of non-adjacent genes on the batholith are through the adjacent ones. However, the mixed model takes a bidimensional viewpoint to simplify the gene relationship, in which each gene makes a direct projection on the surface of the batholith. Given this, in mixed model, it can be inferred that the non-adjacent genes are unavoidable to produce repeated effects on the phenotype (batholith), which, in our opinion, could be used to alternatively explain why too many candidates or QTLs for the same trait had been reported but most of which are hitherto unidentifiable. A. In mixed model, the projected area could be denotative of the effect size of gene. The overlapped projection on the surface of the batholith reflects the interlocus interaction, where the two-time and three-time projection overlapping denotes the one-order and two-order interactions, respectively. For the intralocus interaction (not reflected here), considering the diploid organism in which a gene has two alleles, the interaction can be also expressed by the varied projection area of two alleles along with different combination of alleles. B. In network model, some regulatory links between genes are development-dependent, which dynamically exist at specific developmental stages. The network model is dynamic rather than static.
4. Logical consideration of systems quantitative genetics
4.1. Predictability on the genetic architecture
From the standpoint of scientific philosophy, a stronger prediction power is a crucial criterion to adjust or overturn the old theory to become a new science theory (Kuhn, 1970). As we know, there frequently happened the interstudy discrepancy or paradoxical phenomena for major gene identification or QTLs mapping in the same traits. For such dilemma, except the obscure interpretations such as sampling error and genetic background difference, the molecular quantitative genetics based on the mixed model cannot provide sound explanation or solution. As a major deficiency, the molecular quantitative genetics could only provide a passive detection of the major genes or QTLs of certain traits under certain genetic background. It cannot provide active predictions concerning the status or changes of genetic architectures of target traits. On the contrary, the network model itself declares a network relationship of quantitative trait genes, and once the network model is built up, the output behavior of the network induced by external and/or internal factors can be reliably predicted on its own initiative. In theory, the network model could make active prediction on the genetic architectures of target traits under different genetic background. According to Kuhn, the replacement of the mixed model by the network one would be basically in agreement with the basic rule of science development. Undoubtedly, based on the network model, systems quantitative genetics has a more powerful capability of prediction on the genetic architectures of target traits.
4.2. Controllability on the non-additive genetic effects
It is believed that, due to the scientific advancement of the network model, the theories of systems quantitative genetics would be more advanced than that of earlier generation quantitative genetics, and one aspect of which might be reflected by the biological explanation and controllable manipulation of non-additive genetic effects. There was a fact that the dominance and epistasis pertaining to non-additive genetic effects were statistically rather than biologically described under the theories of classical and molecular quantitative genetics. As it was historically and is presently utilized, the term interaction has been coined to describe the molecular mechanism of non-additive genetic effects [70], in which two types of interactions, i.e., intralocus interactions (dominance) and interlocus interactions (epistasis), were included. However, the concept interaction in the framework of earlier generation of quantitative genetics is quite inexplicit, which abstractively makes a very ambiguous expression without giving distinct biological definitions of them. In contrast, in the framework of network model, the dominance and epistasis components have a clear mechanistic understanding. For instances, Gjuvsland et al. (2007) stated that epistasis was one of the generic characteristics of gene regulatory networks, and presented 19 forms of interaction modules to embody the biological meanings of epistasis [71], and Omholt et al. (2000) declared that the intralocus dominance could be denotative of the negative and positive autoregulatory feedback loops, and the interlocus dominance was intimately connected to either feedback-mediated epistasis or downstream-mediated epistasis [72].
As discussed above, for the ability for providing passive detection rather than active prediction on the genetic architectures of target traits, the molecular quantitative genetics is nearly incapable to take complete control of the non-additive genetic effects in current breeding programs. Although so, it could not deny that the non-additive genetic effects are essentially controllable. In reality, many research articles have documented that there exists a widening consensus about the evolutionary operability of non-additive genetic components [73-80], which, by some measures, illuminates the non-additive components are likely to be favored by natural selection [81] and thus there is a real existence of the operability of the non-additive genetic components in evolution. It is well known that artificial selection is analogous to, or even more intense and effective than natural selection [82]. Therefore, in theory, due to the powerful prediction capability to the genetic architectures of target traits, the more advanced systems quantitative genetics would midwife the birth of a new discipline -- systems breeding that can design an exercisable scheme to provide a better controllability to perform operation on the non-additive genetic effects in future breeding programs.
5. Future directions: what issues will be explored?
It is expected that there will be more daunting mathematical challenges for the future development of systems quantitative genetics. Nevertheless, the expectable mathematical difficulties being faced by systems quantitative genetics should not prevent us from foreseeing ahead the possible issues, though even the molecular quantitative genetics is now under development during both the peak period of theory researches and the rising period of application researches. In our opinion, some of the future researches in systems quantitative genetics might cover the followings:
(i) Basic conceptual framework of the systems quantitative genetics, including semantic representations and the mathematical annotations of terminological systems of new and updated concepts.
(ii) Theories compendium in this field, consisting of the theorem's hypotheses, new biological interpretations of genetic basis of complex and quantitative traits, and the settlement of backward compatibility of the completely new or updated theories to the earlier-generational ones, etc.
(iii) Model developments for estimating the parameters that control the dynamics of genetic networks, involving in complex and alternatively simplified or empirical model designs beyond the traditional linear models; introduction, development and realization of higher-dimensional algorithms such as large scale parallel algorithm and composite machine-learning algorithm to break the expectable mathematical difficulties; genetic network reconstructions and the corresponding evaluation theories, e.g., the intragenerational and intergenerational inheritance rules of Mendelian and non-Mendelian factors under the framework of dynamic network model, the assembly or conditional combination of the full-level information from DNA variome to phenome, identification of network components or parameters associated with the heritable components and noises of target phenotypes; etc.
(iv) The promising application topics such as solutions of breeding or evolutionary issues from systems quantitative genetic perspective, e.g., establishments of systems breeding and systems evolutionary theories in biological sense; development and compilation of software tools; and other extension applications in various fields.
6. Conclusions
A paradigm shift is occurring in the field of quantitative genetics. Until now, some researches to grasp the issues pertaining to systems quantitative genetics but being mainly solved from the view of molecular quantitative genetics have been done [16-18]. Focusing on a causal understanding of how gene expression affects phenotypic measurements, other stirring works beyond genetical genetics [20-23] [41-45] [83] [84] have preliminarily seen the embryo of systems quantitative genetics. In conclusion, in this review article, the marriage of systems biology and quantitative genetics was made to contribute the new understanding of the future development of quantitative genetics, though some points addressed by us, especially the updates of network model and the future shape of the coming systems quantitative genetics, might be partially controversial. In our opinion, systems quantitative genetics is a burgeoning field in its infancy in which many issues that we have not covered might be unpredictable given its current plight. However, it can be quite surely prognosticated that the developments of the theory and method of systems quantitative genetics will open up a whole new area of quantitative genetics.
Acknowledgements
This work was supported by key project of National Natural Science Foundation of China (U0631005), National High Technology Research and Development Program (2006AA10Z195, 2007AA10Z148) of China, and the Key Project of National Basic Research and Developmental Plan (2006CB102105) of China.
Conflict of interest
The authors have declared that no conflict of interest exists.
References
1. Friedman A, Perrimon N. Genetic screening for signal transduction in the era of network biology. Cell. 2007;128:225-31
2. Hiesinger PR, Hassan BA. Genetics in the age of systems biology. Cell. 2005;123:1173-74
3. Kirschner MW. The meaning of systems biology. Cell. 2005;121:503-4
4. Stinchcombe JT, Hoektsra HE. Combining population genomics and quantitative genetics: finding the genes underlying ecologically important traits. Heredity. 2008;100:158-70
5. Steppan SJ, Phillips PC, Houle D. Comparative quantitative genetics: evolution of the G matrix. Trends Ecol Evol. 2002;17:320-27
6. Zhu MJ, Ding JT, Liu B. et al. Estimation of genetic parameters for four reproduction component traits in two Chinese indigenous pig breeds. Asian-Aust J Anim Sci. 2008;21:1109-15
7. Wehner JM, Radcliffe RA, Bowers BJ. Quantitative genetics and mouse behavior. Annu Rev Neurosci. 2001;24:845-67
8. Frankham R. Quantitative genetics in conservation biology. Genet Res. 1999;74:237-44
9. Jorde LB. Linkage disequilibrium and the search for complex disease genes. Genome Res. 2000;10:1435-44
10. Rogers J, Mahaney MC, Almasy L. et al. Quantitative trait linkage mapping in anthropology. Yrbk Phys Anthropol. 1999;42:127-151
11. Burt C. Quantitative genetics in psychology. Br J Math Stat Psychol. 1971;24:1-21
12. Falconer DS, Mackay TFC. Introduction to quantitative genetics, 4th ed. Harlow: Longman Limited. 1996
13. Lynch M, Walsh B. Genetics and analysis of quantitative traits. Sunderland, MA: Sinauer Associates. 1997
14. Zhu MJ, Zhao SH. Candidate gene identification approach: progress and challenges. Int J Biol Sci. 2007;3:420-7
15. Richards EJ. Inherited epigenetic variation--revisiting soft inheritance. Nat Rev Genet. 2006;7:395-401
16. Rattink AP, De Koning DJ, Faivre M. et al. Fine mapping and imprinting analysis for fatness trait QTLs in pigs. Mamm Genome. 2000;11:656-61
17. Clapcott SJ, Teale AJ, Kemp SJ. Evidence for genomic imprinting of the major QTL controlling susceptibility to trypanosomiasis in mice. Parasite Immunol. 2000;22:259-63
18. Jungerius BJ, van Laere AS, Te Pas MF. et al. The IGF2-intron3-G3072A substitution explains a major imprinted QTL effect on backfat thickness in a Meishan x European white pig intercross. Genet Res. 2004;84:95-101
19. Johannes F, Colot V, Jansen RC. Epigenome dynamics: a quantitative genetics perspective. Nat Rev Genet. 2008;9:883-90
20. Sironen A, Thomsen B, Andersson M. et al. An intronic insertion in KPL2 results in aberrant splicing and causes the immotile short-tail sperm defect in the pig. Proc Natl Acad Sci USA. 2006;103:5006-11
21. Schadt EE, Lamb J, Yang X. et al. An integrative genomics approach to infer causal associations between gene expression and disease. Nat Genet. 2005;37:710-17
22. Livshits G. Quantitative genetics of circulating molecules associated with bone metabolism. J Musculoskelet Neuronal Interact. 2006;6:47-61
23. Stylianou IM, Affourtit JP, Shockley KR. et al. Applying gene expression, proteomics and single-nucleotide polymorphism analysis for complex trait gene identification. Genetics. 2008;178:1795-805
24. Zhu MJ, Zhao SH. Systems quantitative genetics: the coming third generation of quantitative genetics. In: (ed.) Weir BS, Hill WG, Zhu J. et al. The Third International Conference of Quantitative Genetics. Hangzhou, China. 2007:135
25. Aylor DL, Zeng ZB. From classical genetics to quantitative genetics to systems biology: modeling epistasis. PLoS Genet. 2008;4:e1000029
26. Jansen R C, Nap JP. Genetical genomics: the added value from segregation. Trends Genet. 2001;17:388-91
27. de Koning DJ, Haley CS. Genetical genomics in humans and model organisms. Trends Genet. 2005;21:377-81
28. Morley M, Molony CM, Weber TM. et al. Genetic analysis of genome-wide variation in human gene expression. Nature. 2004;430:743-7
29. Gibson G, Weir B. The quantitative genetics of transcription. Trends Genet. 2005;21:616-23
30. Brew RB, Yvert G, Clinton R. et al. Genetic dissection of transcriptional regulation in budding yeast. Science. 2002;296:752-5
31. Schadt EE, Monks SA, Drakes TA. et al. Genetics of gene expression surveyed in maize, mouse and man. Nature. 2003;422:297-302
32. Göring HH, Curran JE, Johnson MP. et al. Discovery of expression QTLs using large-scale transcriptional profiling in human lymphocytes. Nat Genet. 2007;39:1208-16
33. West MA, Kim K, Kliebenstein DJ. et al. Global eQTL mapping reveals the complex genetic architecture of transcript-level variation in Arabidopsis. Genetics. 2007;175:1441-50
34. Dixon AL, Liang L, Moffatt MF. et al. A genome-wide association study of global gene expression. Nat Genet. 2007;39:1202-7
35. Hull J, Campino S, Rowlands K. et al. Identification of common genetic variation that modulates alternative splicing. PLoS Genet. 2007;3:e99
36. Keurentjes JJ, Fu J, Terpstra IR. et al. Regulatory network construction in Arabidopsis by using genome-wide gene expression quantitative trait loci. Proc Natl Acad Sci USA. 2007;104:1708-13
37. Ferrara CT, Wang P, Neto EC. et al. Genetic networks of liver metabolism revealed by integration of metabolic and transcriptional profiling. PLoS Genet. 2008;4:e1000034
38. Al-Shahrour F, Díaz-Uriarte R, Dopazo J. Discovering molecular functions significantly related to phenotypes by combining gene expression data and biological information. Bioinformatics. 2005;21:2988-93
39. Williams RB, Chan EK, Cowley MJ, Little PF. The influence of genetic variation on gene expression. Genome Res. 2007;17:1707-16
40. Wentzell AM, Rowe HC, Hansen BG. et al. Linking metabolic QTL with network and cis-eQTL controlling biosynthetic pathways. PLoS Genet. 2007;3:e162
41. Chen Y, Zhu J, Lum PY. et al. Variations in DNA elucidate molecular networks that cause disease. Nature. 2008;452:429-35
42. Mehrabian M, Allayee H, Stockton J. et al. Integrating genotypic and expression data in a segregating mouse population to identify 5-lipoxygenase as a susceptibility gene for obesity and bone traits. Nat Genet. 2005;37:1224-33
43. Chesler EJ, Lu L, Shou S. et al. Complex trait analysis of gene expression uncovers polygenic and pleiotropic networks that modulate nervous system function. Nat Genet. 2005;37:233-42
44. Emilsson V, Thorleifsson G, Zhang B. et al. Genetics of gene expression and its effect on disease. Nature. 2008;452:423-8
45. Dermitzakis ET. From gene expression to disease risk. Nat Genet. 2008;40:492-3
46. Wu RL. Mapping quantitative trait loci by genotyping haploid tissues. Genetics. 1999;152:1741-52
47. Liu Z, Dekkers JC. Least squares interval mapping of quantitative trait loci under the infinitesimal genetic model in outbred populations. Genetics. 1998;148:495-505
48. Zhang YM, Gai J. Methodologies for segregation analysis and QTL mapping in plants. Genetica. 2008 [Epub ahead of print]
49. Elkind Y, Cahaner A. A mixed model for the effects the major gene and polygenes on tomato fruit softness. Heredity. 1990;64:205-13
50. Xu S. Estimating polygenic effects using markers of the entire genome. Genetics. 2003;163:789-801
51. Lou XY, Zhu J. Analysis of genetic effects of major genes and polygenes on quantitative traits I. Genetic model for diploid plants and animals. Theor Appl Genet. 2002;104:414-21
52. Bentsen HB. Polygenic inheritance. In: (ed.) Gjedrem T. Selection and Breeding Programs in Aquaculture. Dordrecht, Netherlands: Springer Publishers. 2005:35-43
53. Lande R. The influence of the mating system on the maintenance of genetic variability in polygenic characters. Genetics. 1977;86:485-98
54. Thompson JN. Quantitative variation and gene numbers. Nature. 1975;258:525
55. Xiao J, Wang X, Hu Z. et al. Multivariate segregation analysis for quantitative traits in line crosses. Heredity. 2007;98:427-35
56. Frank SA. Genetic variation of polygenic characters and the evolution of genetic degeneracy. J Evol Biol. 2003;16:138-42
57. Gai JY, Wang JK. Identification and estimation of a QTL model and its effects. Theor Appl Genet. 1998;97:1162-8
58. Zhuang Y, Adams KL. Extensive allelic variation in gene expression in populus F1 hybrids. Genetics. 2007;177:1987-96
59. Xiao J, Li J, Yuan L, Tanksley SD. Dominance is the major genetic basis of heterosis in rice as revealed by QTL analysis using molecular markers. Genetics. 1995;140:745-54
60. Zhang L, Li H, Li Z. et al. Interactions between markers can be caused by the dominance effect of QTL. Genetics. 2008;180:1177-90
61. He XH, Zhang YM. Mapping epistatic quantitative trait loci underlying endosperm traits using all markers on the entire genome in a random hybridization design. Heredity. 2008;101:39-47
62. Yi N, Yandell BS, Churchill GA. et al. Bayesian model selection for genome-wide epistatic quantitative trait loci analysis. Genetics. 2005;170:1333-44
63. Yang J, Zhu J, Williams RW. Mapping the genetic architecture of complex traits in experimental populations. Bioinformatics. 2007;23:1527-36
64. Carlborg O, Hocking PM, Burt DW, Haley CS. Simultaneous mapping of epistatic QTL in chickens reveals clusters of QTL pairs with similar genetic effects on growth. Genet Res. 2004;83:197-209
65. Ming R, Del Monte TA, Hernandez E. et al. Comparative analysis of QTLs affecting plant height and flowering among closely-related diploid and polyploid genomes. Genome. 2002;45:794-803
66. Korol AB, Ronin YI, Nevo E. Approximate analysis of QTL-environment interaction with no limits on the number of environments. Genetics. 1998;148:2015-28
67. Piepho HP. A mixed-model approach to mapping quantitative trait loci in barley on the basis of multiple environment data. Genetics. 2000;156:2043-50
68. Guss KA, Nelson CE, Hudson A. et al. Control of a genetic regulatory network by a selector gene. Science. 2001;292:1164-7
69. Elowitz MB, Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335-8
70. Phillips PC. The language of gene interaction. Genetics. 1998;149:1167-71
71. Gjuvsland AB, Hayes BJ, Omholt SW. et al. Statistical epistasis is a generic feature of gene regulatory networks. Genetics. 2007;175:411-20
72. Omholt SW, Plahte E, Oyehaug L. et al. Gene regulatory networks generating the phenomena of additivity, dominance and epistasis. Genetics. 2000;155:969-80
73. Bagheri HC, Wagner GP. Evolution of dominance in metabolic pathways. Genetics. 2004;168:1713-35
74. Doebley J, Stec A, Gustus C. teosinte branched1 and the origin of maize: evidence for epistasis and the evolution of dominance. Genetics. 1995;141:333-46
75. Bomblies K, Doebley JF. Pleiotropic effects of the duplicate maize FLORICAULA/LEAFY genes zfl1 and zfl2 on traits under selection during maize domestication. Genetics. 2006;172:519-31
76. Doebley J, Stec A, Hubbard L. The evolution of apical dominance in maize. Nature. 1997;386:485-8
77. Le Rouzic A, Alvarez-Castro JM, Carlborg O. Dissection of the genetic architecture of body weight in chicken reveals the impact of epistasis on domestication traits. Genetics. 2008;179:1591-9
78. Kelly JK. Epistasis in Monkeyflowers. Genetics. 2005;171:1917-31
79. Bradshaw WE, Haggerty BP, Holzapfel CM. Epistasis underlying a fitness trait within a natural population of the pitcher-plant mosquito, Wyeomyia smithii. Genetics. 2005;169:485-8
80. Weinreich DM, Watson RA, Chao L. Perspective: sign epistasis and genetic constraint on evolutionary trajectories. Evolution. 2005;59:1165-74
81. Desai MM, Weissman D, Feldman MW. Evolution can favor antagonistic epistasis. Genetics. 2007;177:1001-10
82. Falk R. Between beanbag genetics and natural selection. Biol Philos. 1990;5:313-25
83. Ferkingstad E, Frigessi A, Lyng H. Indirect genomic effects on survival from gene expression data. Genome Biol. 2008;9:R58
84. Nica AC, Dermitzakis ET. Using gene expression to investigate the genetic basis of complex disorders. Hum Mol Genet. 2008;17:R129-34
Author contact
![]() Correspondence to: Shuhong Zhao, Key Laboratory of Agricultural Animal Genetics, Breeding and Reproduction of Ministry of Education, Huazhong Agricultural University, Wuhan 430070, P. R. China; Tel: +86-27-87284161; Fax: +86-27-87280408; E-mail: shzhaohzau.edu.cn
Correspondence to: Shuhong Zhao, Key Laboratory of Agricultural Animal Genetics, Breeding and Reproduction of Ministry of Education, Huazhong Agricultural University, Wuhan 430070, P. R. China; Tel: +86-27-87284161; Fax: +86-27-87280408; E-mail: shzhaohzau.edu.cn

 Global reach, higher impact
Global reach, higher impact