10
Impact Factor
ISSN: 1449-2288
Int J Biol Sci 2013; 9(10):1050-1056. doi:10.7150/ijbs.7242 This issue Cite
Research Paper
Simulation of Interstitial Fluid Flow in Ligaments: Comparison among Stokes, Brinkman and Darcy Models
Department of Mechanics and Engineering Science, Fudan University, Shanghai Research Center of Acupuncture, Shanghai, 200433.
Received 2013-7-24; Accepted 2013-9-27; Published 2013-11-5
Abstract
In this paper, we use Stokes, Brinkman and Darcy equations to approximate the porous continuum media of ligament tissues respectively, simulate the flow field with FLUENT software, and study the shear stress on the cell surface due to the interstitial fluid flow. Since the Brinkman equation approaches Stokes equation well in high hydraulic permeability (kp) condition (kp ≥1.0×10-8 m2 in our numerical simulation), and it is an approximation to Darcy model in low kp condition (kp ≤5.0×10-12 m2 in our numerical simulation), we used the Brinkman model to simulate the interstitial fluid flow in the ligament where kp is approximately 1.0×10-16 m2. It shows kp and anisotropic property have a little effect on the flow field, but have a great effect on the shear stress on the membrane of interstitial cells (τcell). There is a linear relationship between τcell and 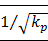 , when kp =1.0×10-16 m2 and the maximum τcell (τcell,max) is approximately 10 Pa. The anisotropic property will affect τcell's distribution on the cell surface. When kx/ky>1, low τcell dominates the cell, while when kx/ky<1, high τcell dominants the cell.
, when kp =1.0×10-16 m2 and the maximum τcell (τcell,max) is approximately 10 Pa. The anisotropic property will affect τcell's distribution on the cell surface. When kx/ky>1, low τcell dominates the cell, while when kx/ky<1, high τcell dominants the cell.
Keywords: Interstitial fluid flow, porous media, numerical simulation, sheer stress, anisotropy.
Introduction
The interstitium is the space located between the capillary walls and the cells. The basic structure of the interstitium is similar in all tissues: collagen builds a fibril framework that is full of interstitial fluid; interstitial cells are distributed in interstitium. The components of interstitial fluid are very complex, including water, glycosaminoglycan, proteoglycan, proteins and so on. The interstitial fluid volume is as much as approximately 3 times of the blood's volume. Interstitial fluid contacts with the cells more directly than blood does. But the researches on interstitial fluid are fewer than those on blood. Not only the components of interstitial fluid but also its flow plays an important role in the tissue's normal physiological activities [1, 2]. In poorly vascularized tissues such as ligaments and tendons, the flow of interstitial fluid is especially important.
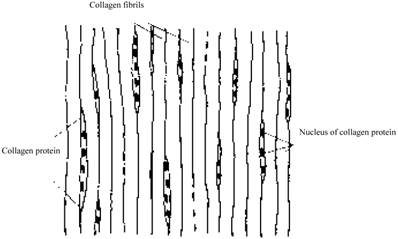
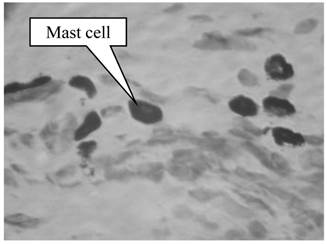
Many factors are known to influence the flow of interstitial fluid. First, interstitial fluid and blood exchange occurs at the capillary walls [3]. Therefore, the flow of interstitial fluid is affected by the conformation of capillaries and the penetrating velocity on the wall of capillaries. Second, the space of the interstitium is not empty but full of collagen fibril network, which affects the flow of interstitial fluid. In different tissues the structure of the collagen fibrils are different. For example, in derma, collagen fibrils are organized into meshes and in ligaments, into regular parallel arrays, as shown in Fig. 1 [4]. Third, interstitial cells also affect the interstitial flow. In brain, neurons and glial cells formed the tight central nervous system (CNS) [5], while in the stained connective tissue, interstitial cells (Mast cells, MCs) are isolated (×400, Fig.2).
Configuration of parallel collagen fibrils.
MCs in the skin under electron microscope. One dark circle represents one cell
Most mathematical models of interstitial flow through fibrous matrix to date present the tissue as a continuum space and Stokes, Brinkman and Darcy equations are adopted respectively to study the interstitial fluid flow [6-9]. For example, Lee and Fung [6] used Stokes equation to study a thin boundary-layer region near the fibrils surface. Pedersen et al. [7, 8] and we [9] used Brinkman equation to study the soft tissue. Chen et al. [10] used Darcy equation to study the interstitial fluid flow in ligaments and tendons. In Brinkman and Darcy equations, the properties of the fibrous matrix are represented by a hydraulic permeability kp that averages the flow resistance offered by the porous media across the entire flow domain. Many factors affect the tissue permeability; therefore, it's hard to determine its accurate value which has to be evaluated in most cases. Yet, through numerical simulation, the estimated values of different cases are widely distinguished, ranging from 1.0×10-10 m2 to 1.7×10-17 m2 [7, 9].
In this paper, based on a simple coupled capillariy-interstitium model, we take a computational fluid dynamics (CFD) approach to investigate the following problems: (i) comparison of three equations (Stokes, Brinkman and Darcy) numerical results; (ii) the effect of kp on the interstitial fluid flow and interstitial cells; (iii) the effect of interstitial cells on the flow field; (iv) the effect of the ratio of longitudinal permeability kx (parallel to the collagen fibrils) to the transverse permeability ky (perpendicular to the collagen fibrils) (ratio=kx/ky) on the interstitial fluid flow and interstitial cells.
Mathematical Model and Methods
Model
The two-dimensional interstitial fluid domain is occupied by a porous media, the top and the bottom of which are the capillaries (Fig.3). The capillaries collocate parallelly in the x direction: the left side of the capillary is near the arteriole, and the right side of the capillary is near the venule. We denote 2H as the distance between two neighboring capillaries and L as the length of the capillary. The four short lines at the four corners represent periodic conditions and the lengths of the lines are 0.01 L.
A coupled capillariy-interstitium model.

To solve the mathematical model, we need to determine the boundary conditions. Denote  the velocity, p the pressure, ρ the density, μ the viscosity. Assuming that before entering and after leaving the domain, the flow is fully-developed and the derivative of horizontal velocities at the inlet and outlet are zero, namely,
the velocity, p the pressure, ρ the density, μ the viscosity. Assuming that before entering and after leaving the domain, the flow is fully-developed and the derivative of horizontal velocities at the inlet and outlet are zero, namely,
(1)
Unfortunately, these conditions result in the ill-posedness of the problem. To overcome this flaw, we subtract a background flow to fix the horizontal velocity at the inlet (x=-0.01 L) to zero. On the other hand, at the top and bottom of the interstitial space, we adopt the well-accepted Starling formula [3]
(2)
where kc is the permeability coefficient of capillary's wall, pi is the interstitial hydrostatic pressure at the capillary wall, πc is the osmotic pressure in blood, and πi is the interstitial osmotic pressure at the capillary wall. Here, according to the Poiseuille's Law [3], pc will decrease linearly from artery to vein, assuming other parameters are constants. Finally, we impose the nonslip condition along the capillary walls (ux=0).
In order to study the effect of cells on interstitial flow and the effect of flow on interstitial cells, we place a cell (a circle with diameter of 8μm) in the center of the domain and impose the nonslip condition on the cell's wall (ux= uy=0). The sheer stress on the mast cell (τcell) is
(3)
Stokes equation
Assuming the interstitial fluid is incompressible and defining the dimensionless parameters 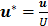 ,
, 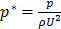 ,
,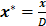 , the continuity equation is
, the continuity equation is
(4)
where U is the characteristic velocity, defined as 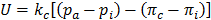 , pa is the hydrostatic pressure at the arteriole section of capillary, D is the diameter of capillaries, and
, pa is the hydrostatic pressure at the arteriole section of capillary, D is the diameter of capillaries, and 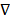 is the gradient operator. Generally, the steady viscous fluid dynamics equation is the Navier-Stokes equation
is the gradient operator. Generally, the steady viscous fluid dynamics equation is the Navier-Stokes equation
(5)
where 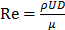 is the Reynolds number, and
is the Reynolds number, and 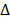 is the Laplacian operator. Because Re is small (approximately 10-6 in this model), the inertia term (
is the Laplacian operator. Because Re is small (approximately 10-6 in this model), the inertia term ( ) is negligible compared to the viscous term (
) is negligible compared to the viscous term ( ). Then the Navier-Stokes equation is simplified as the Stokes equation
). Then the Navier-Stokes equation is simplified as the Stokes equation
(6)
Brinkman and Darcy equations
Low Reynolds number flows in porous media filled with a matrix of fibrous material have frequently been approximated using a Brinkman equation, and the properties of the material are represented by a hydraulic permeability 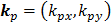 [11]. Pederson et al. [7] evaluated that kp ranged from approximately 4.0×10-11 m2 to 1.0×10-13 m2 in tissues, while Chen et al. [10] estimated that kp ranged from 1.0×10-16 m2 to 1.0×10-18 m2 in ligaments. Define
[11]. Pederson et al. [7] evaluated that kp ranged from approximately 4.0×10-11 m2 to 1.0×10-13 m2 in tissues, while Chen et al. [10] estimated that kp ranged from 1.0×10-16 m2 to 1.0×10-18 m2 in ligaments. Define  , the dimensionless Brinkman equation is
, the dimensionless Brinkman equation is
(7)
when 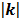 is small, the viscous term (
is small, the viscous term (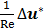 ) is negligible compared to the Darcy-Forchheimer term (
) is negligible compared to the Darcy-Forchheimer term (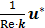 ) and Brinkman equation reduces to Darcy's law [11],
) and Brinkman equation reduces to Darcy's law [11],
(8)
Computational method
The CFD software package FLUENT (version 6.0) is used for the numerical simulation. The grid is generated by the GAMBIT software package. The governing equations are solved by iterating. When the iteration is convergent (error of iterated results e<0.001), the velocity field is obtained.
Physiological parameters
Table 1 shows the physiological parameters used in the numerical simulation. Based on these values, the characteristic velocity U=1.33×10-6 m/s.
Physiological parameter values of the model.
| Parameter | Value |
|---|---|
| Viscosity of interstitial fluid μ/( kg·m-1·s-1) | 3.5×10-3 [10] |
| Permeability coefficient of capillary's wall kc /( m2·s·kg-1) | 5×10-10 [13] |
| Plasma colloid osmotic pressure πc /mmHg | 28 [3] |
| Interstitial colloid osmotic pressure at the capillary wall πi /mmHg | 8 [12] |
| Density of interstitial fluid ρ /(kg·m-3) | 1000[3] |
| Length of capillary L/μm | 1000[3] |
| Diameter of capillary D/μm | 8[3] |
| Distance between adjacent capillaries (2H)/μm | 48[3] |
| Interstitial hydrostatic pressure at the capillary wall pi/mmHg | -5 [12] |
| Hydrostatic pressure at the arteriole section of capillary pa /mmHg | 30 [3] |
| Hydrostatic pressure at the venule section of capillary pv /mmHg | 10 [3] |
Results
Interstitial flow filed in isotropic media
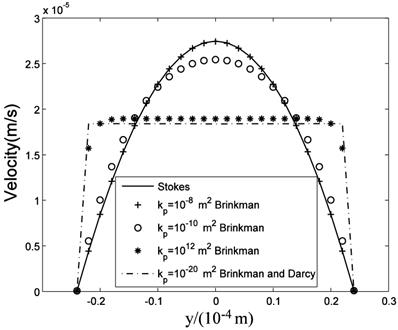
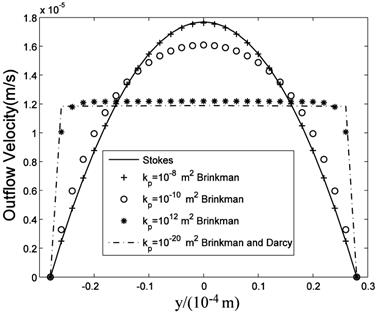
The computational results of Stokes equation and Brinkman equation are nearly the same when kp is large (Fig.4, kp=1×10-8m2, display scale is x:y=1:5), while the results of Darcy equation and Brinkman equation are similar when kp is small (Fig.5, kp=5×10-12m2, display scale is x:y=1:5). The numerical results of Stokes, Brinkman and Darcy equations all show that the interstitial fluids flow from the capillary to the interstitium at the arteriole (left) side and are absorbed by the capillaries at the venule (right) side. Near the x axis (symmetry axis, y=0), the flows' directions tend to become parallel to the capillaries, and the maximum velocities are at the x axis (x≈660μm). The maximum velocities of Stokes and Brinkman (kp=1×10-8m2) equations are 2.75×10-5 m/s, while the maximum velocities of Darcy and Brinkman (kp=5×10-12m2) equations are 2.01×10-5 m/s. The velocity profile in the cross-section causes the difference between the maximum velocities: the velocity profile of Stokes equation is the parabola shape, which is accordance with Fu et al.'s μPIV measurement [14] ('+'and 'o' in Fig.6 and Fig.7), while the velocity profile of Darcy equation is nearly equality ('*' and dash-dot line in Fig.6 and Fig.7). The results also show there are boundary layers in Brinkman equation, and the thickness of the boundary layers is positive correlation to kp ('*' and dash-dot line in Fig.6 and Fig.7).
Interstitial flow field in isotropic media (a) Brinkman equation (kp=1×10-8m2), (b) Stokes equation.
Interstitial flow field in isotropic media (a) Brinkman equation (kp=5×10-12m2), (b) Darcy equation
velocity profile in the maximum velocity cross-section (x=0.66mm).
velocity profile at the outlet (x=1mm) .
The effect of interstitial cells on the flow field
Fig.8 is the flow field near the cell (Brinkman equation, kp=1×10-12m2). The interstitial cell has little effect on the flow field except for the flow field near the cell surface where a boundary layer exists. Interstitial fluid velocity will provide mechanical stimuli to the interstitial cell, and the sheer stress on the surface of cell (τcell) is direct proportional to 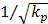 because of Brinkman boundary layer (Fig.9). Fig.10 shows the cell's influence is approximately 10 μm range, where '+' and '*' represent the velocities in the cross-sections of 2 μm before and after the cell respectively. There are obviously a large variation at |y|<10μm range. 'o' represents the velocity in the cross-section of 10 μm before the cell. There is a slightly change at |y|<10μm range. The solid line represents the velocity in the cross-section of 20 μm before the cell, and it is similar to the velocity without the interstitial cell (dash-dot line in Fig.6).
because of Brinkman boundary layer (Fig.9). Fig.10 shows the cell's influence is approximately 10 μm range, where '+' and '*' represent the velocities in the cross-sections of 2 μm before and after the cell respectively. There are obviously a large variation at |y|<10μm range. 'o' represents the velocity in the cross-section of 10 μm before the cell. There is a slightly change at |y|<10μm range. The solid line represents the velocity in the cross-section of 20 μm before the cell, and it is similar to the velocity without the interstitial cell (dash-dot line in Fig.6).
The flow field near the cell (Brinkman equation, kp=1×10-12m2).

τcell distribution at the cell surface.
Velocities in the cross-sections.

Interstitial flow filed in anisotropic media
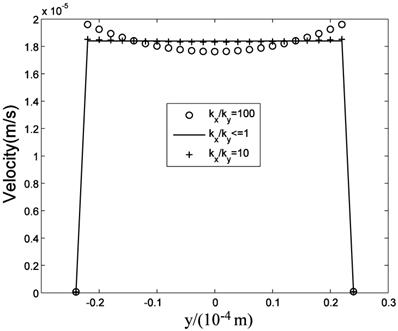
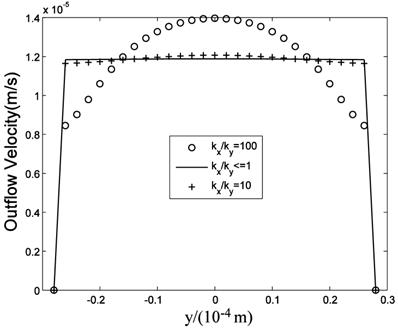
While many researches assumed the tissue is isotropic, Chen et al. [10] showed the parallel arrangement of collagen fibrils in ligaments will certainly lead to anisotropic permeability property in the tissue. Our simulation results showed that the flow fields are similar when kx is equal to or less than ky, that is when kx/ky ≤1, while the flow fields are different when kx>ky. Fig.11 is the velocity in the maximum velocity cross-section, which shows the velocity profile is more concave-down with the ratio increase. Fig.12 plots the velocity at the outlet, which shows the velocity profile is more convex with the ratio increase. Though anisotropic property will affect the flow field, Fig.11 and Fig.12 show the influence is less when kx/ky<10, and the influence is not great even when kx/ky=100. Based on Chen et al.'s results, the maximum evaluation value of ratio in ligaments is less than 50 [10]. Therefore, the isotropic analysis in some research is acceptable.
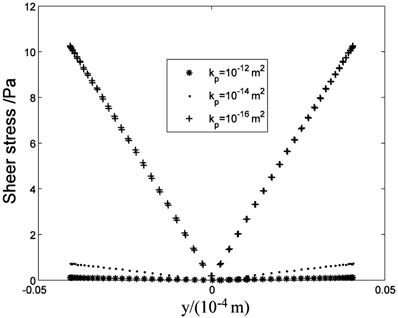
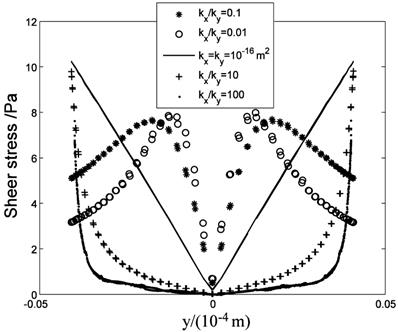
The anisotropic property will affect the flow field near the cell surface and τcell obviously. Fig.13 shows the low τcell range increases with ratio increasing, and the maximum τcell is at y=±4μm (the top and bottom sides of the cell) when kx/ky>1. When kx/ky=100, τcell at over 85% range of the cell surface(y<±3.3 μm) is under 1 Pa, and τcell increases to 10 Pa quickly near y=±4μm position ('·' in Fig.13). When kx/ky<1, the positions of maximum τcell shift to the left and right sides of the cell and the high τcell range increases ('*' and 'o' in Fig.13, y=0μm represent the left and right sides of the cell).
Velocities in the maximum velocity cross-section.
Velocity distribution at the outlet.
τcell distribution at the cell surface.
Discussion and Conclusions
In this study, we explore the nature of interstitial fluid flow in ligaments and compare the results derived from Stokes, Brinkman and Darcy models. Through the simulations, we can make the following conclusions.
Parallel array capillaries can induce parallel interstitial fluid flow no matter which model is selected
The interstitial fluid flow is nearly parallel to the capillaries. The difference between these models is the velocity distribution in the cross-section: parabola shape in Stokes model and uniform in Darcy model. The numerical simulation is accordance with the analytical solutions [11]: Brinkman equation approaches Stokes equation well in high kp condition (kp ≥1.0×10-8 m2), while is an approximation to Darcy model in low kp condition (kp ≤5.0×10-12 m2), except for that there exist a boundary layer of 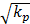 magnitude. One group of capillaries will generate 1.2×10-5 m/s (0.07cm/min) velocity at the outlet. If the fluid from the capillaries is not absorbed by lymphatic, it will flow downstream and be accelerated through the next group of capillaries. In the past, it was accepted that the most seepage from the arteriole side of capillary is absorbed at the venule side of capillary, and the surplus is absorbed by lymphatic vessels right away. Since lymphatic vessels are not always near capillary and the seepage from arteries is always more than the fluid absorbed by capillaries, the unabsorbed fluid will travel some distance and even a long distance before being reabsorbed by capillary or lymphatic. Interstitial fluid flow will affect cells bioactivities. To poorly vascularized tissues such as ligaments and tendons, the flow of interstitial fluid is more important to metabolism.
magnitude. One group of capillaries will generate 1.2×10-5 m/s (0.07cm/min) velocity at the outlet. If the fluid from the capillaries is not absorbed by lymphatic, it will flow downstream and be accelerated through the next group of capillaries. In the past, it was accepted that the most seepage from the arteriole side of capillary is absorbed at the venule side of capillary, and the surplus is absorbed by lymphatic vessels right away. Since lymphatic vessels are not always near capillary and the seepage from arteries is always more than the fluid absorbed by capillaries, the unabsorbed fluid will travel some distance and even a long distance before being reabsorbed by capillary or lymphatic. Interstitial fluid flow will affect cells bioactivities. To poorly vascularized tissues such as ligaments and tendons, the flow of interstitial fluid is more important to metabolism.
Interstitial cells will affect the flow field near the cell surface and interstitial fluid flow can induce shear stress on cell surface
Though the interstitial cell has little effect on the flow field 20 μm away from the cell surface, it does affect the flow field near the cell surface. Therefore, for the interstitial cells that isolated from each other (Fig.2), it is reasonable to neglect other cell's effect when study the shear stress on one cell. Interstitial fluid velocity will induce τcell on the surface of cell in Brinkman equation and τcell is direct proportional to 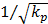 , which is accordance with the theoretical analysis [11].
, which is accordance with the theoretical analysis [11].
The anisotropic property has a little effect on the interstitial fluid flow, but will affect τcell's distribution on the cell surface
The anisotropic property has little effect on the interstitial fluid flow when kx/ky<1, while has some effect on the interstitial fluid flow when kx/ky>1. The increase of kx/ky will induce the velocity profile concave in the cross-section. We don't know the physiological effect of this concave. Weimbum et al. had found the similar drop in the middle of the cross-section when discussing the flow through an orifice in a fibrous medium [15]. The anisotropic property has obvious effect on τcell. When kx/ky>1, low τcell dominates the cell and the maximum τcell is at the top and bottom sides of the cell. When kx/ky<1, high τcell dominants the cell and the positions of maximum τcell shift to the left and right sides of the cell. This results show that the parallel arrangement of fibril along the capillaries (kx/ky>1) can reduce the mechanical stimuli on cells induced by the interstitial fluid flow. In vitro experiments have shown that subtle fluid flow environment plays an important role in cells' living, reproduction and development [16-18]. For example, Swartz et al. found that collagen aligns perpendicular to subtle flow [16], and Hayward et al. figured out that the interstitial fluid velocity and tissue shear stress are key mechanical stimuli for the differentiation of skeletal tissues [18]. But the mechanism of the flow's function is unknown.
This numerical simulation provides an effective way to explore the in vivo interstitial fluid flow in all sorts of tissues, helps to set up the vivid subtle interstitial flow environment of cells, and is benefit to understand the physiological functions of interstitial fluid flow.
Acknowledgements
This work was supported by National natural science foundation of China (11202053), Shanghai Science Foundation (12ZR1401100), and 973 project (2012CB518502).
Competing Interests
The authors have declared that no competing interest exists.
References
1. Grodzinsky AJ, Levenston ME, Jin M. et al. Cartilage tissue remodeling in response to mechanical forces. Annu Rev Biomed Eng. 2000;2:691
2. Swartz MA, Fleury ME. Interstitial Flow and Its Effects in Soft Tissues. Annu Rev Biomed Eng. 2007;9:229-256
3. Keener J, Sneyd J. Mathematical physiology (Second edition). New York, USA: Springer-Verlag. 2009
4. Jozsa L, Kannus P, Balini JB. et al. Three-dimensional ultrastructure of human tendons. Acta Anat. 1991;142:306-312
5. Abbott NJ. Evidence for bulk flow of brain interstitial fluid: significance for physiology and pathology. Neurochem Int. 2004;45:545-552
6. Lee JS, Fung YC. Stokes flow around a circular cylindrical post confined between two parallel plates. J Fluid Mech. 1969;37:657-670
7. Pedersen JA, Boschetti F, Swartz MA. Effects of extracellular fiber architecture on cell membrane shear stress in a 3D fibrous matrix. J Biomech. 2007;40:1484-1492
8. Pedersen JA, Lichter S, Swartz MA. Cells in 3D matrices under interstitial flow: Effects of extracellular matrix alignment on cell shear stress and drag forces. J Biomech. 2010;43:900-905
9. Yao W, Ding GH. Interstitial fluid flow: Simulation of mechanical environment of cells in the interosseous membrane. Acta Mech Sinica-PRC. 2011;27:602-610
10. Chen CT, Malkus DS, Vanderby R. A fiber matrix model for interstitial fluid flow and permeability in ligaments and tendons. Biorheology. 1998;35:103-118
11. Tsay RY, Weinbaum S. Viscous flow in a channel with periodic cross-bridging fibers: Exact solution and Brinkman approximation. J Fluid Mech. 1991;226:125
12. Guyton C, Hall JE. Textbook of Medical Physiology (Eleventh edition). Philadelphia, USA: Elsevier Inc. 2006
13. Hu X, Adamson RH, Liu B. et al. Starling forces that oppose filtration after tissue oncotic pressure is increased. Am J Physiol-Heart C. 2000;279:1724-1736
14. Fu Y, Kunz R, Wu JH. et al. Study of Local Hydrodynamic Environment in Cell-Substrate Adhesion Using Side-View μPIV Technology. PLOS ONE. 2012;7:1-13
15. Feng J, Weinbaum S. Flow through an orifice in a fibrous medium with application to fenestral pores in biological tissue. Chem Eng Sci. 2001;56:5255-5268
16. Ng CP, Hins B, Swartz MA. Interstitial fluid flow induces myofibroblast differentiation and collagen alignment in vitro. J Cell Sci. 2005;118:4731
17. Ng CP, Swartz MA. Mechanisms of interstitial flow-induced remodeling of fibroblast-collagen cultures. Ann Biomed Eng. 2006;34:446
18. Hayward LN, Morgan EF. Assessment of a mechano-regulation theory of skeletal tissue differentiation in an in vivo model of mechanically induced cartilage formation. Biomech Model Mechan. 2009;8:447-455
Author contact
![]() Corresponding author: weiyaoedu.cn.
Corresponding author: weiyaoedu.cn.

 Global reach, higher impact
Global reach, higher impact