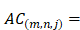Impact Factor
ISSN: 1449-2288
Int J Biol Sci 2018; 14(8):863-871. doi:10.7150/ijbs.24588 This issue Cite
Research Paper
Identification of Inhibitors of MMPS Enzymes via a Novel Computational Approach
1. School of Computer Science and Technology, Tianjin University, Tianjin 300350, China;
2. Tianjin University Institute of Computational Biology, Tianjin University, Tianjin 300350, China;
3. Department of Computer Science and Engineering, University of South Carolina, Columbia, SC 29208, USA;
4. School of Chemical Engineering and Technology, Tianjin University, Tianjin 300350, China.
Received 2017-12-27; Accepted 2018-2-28; Published 2018-5-22
Abstract
Matrix metalloproteases (MMPs) are a family of zinc-dependent proteinases that play complex and diverse roles in metabolism, which are vital for physiological development. In this paper, we present a novel method to identify peptide binding to seven matrix metalloproteases. First, we propose a novel sampling criteria for constructing a training set for each new peptide motif. Then, we select nine physicochemical properties of amino acids and compute their auto-cross covariance to effectively extract features for both natural and non-natural amino acids. Finally, we adopt random forest to predict binding values of each peptide motif respectively with seven MMPs. Our method verifies on 1300 known peptide motifs binding to seven MMPs and achieved preeminent Pearson-product-moment correlation coefficient (PCC) and root mean squared error (RMSE) on all seven MMPs, especially of 0.9181 and 9.3827 on MMP-7. We predict binding values of 4000 peptide motifs and identify peptides preferentially bind to MMP-2 and MMP-7. We herein report 4 novel inhibitor candidates of Asp-Ile-Phe, Asp-Ile-Tyr, Asp-Ile-Lys and Hser-Gly-Phe with high potency and selectivity binding to MMP-2, as well as 6 novel inhibitor candidates of Chg-Ile-Ile, Chg-Ile-Leu, Chg-Ile-Glu, Chg-Ile-Met, Chg-Val-Ile and Chg-Val-Leu selectively binding to MMP-7. Our findings facilitate the identification of inhibitors with good potency as well as desirable selectivity, providing significant insights of candidate inhibitor drugs.
Keywords: MMPs, peptide inhibitors, auto-cross covariance, random forest
Introduction
Matrix metalloproteases (MMPs) are a family of zinc-dependent proteinases that play complex and diverse roles in metabolism, which are vital for physiological development. It has been revealed that MMP-2 and MMP-7 directly accelerate tumori-genesis, which means these enzymes as vital disease targets [1]. On the other side, some members in the MMP family often confer protective effects in various human diseases, improving host resistance towards cancer and other abnormalities [2]. For example, knocking-out certain MMPs (MMPs-3, -8 and -9) has been found directly linked to tumor proliferation in animal models of several cancers, emphasizing the positive roles mediated by selective members of the MMP family [3]. Hence, there have accordingly been intense interests in developing effective small-molecule drugs with strong selectivity against specific negative members of this class of enzymes.
Nevertheless, MMPs have highly conserved mechanisms and share some active sites. Several MMP inhibitors which were at first selected and optimized on the basis of good potency came into extensive phase III clinical trials, only to be discovered ineffective because of problems arising from a lack of selectivity [4]. This raises a major impetus and a big challenge to develop compounds with not only good potency but also high selectivity [5]. Ideally, such inhibitors should inhibit only target MMPs (MMP-2 and MMP-7) responsible for the relevant disease, while minimally affecting any anti-target MMPs (MMP-3, MMP-8 and MMP-9), which may be beneficial for human-being.
There have been several experimental strategies proposed in order to address these pressing challenges. Rao et.al proposed a well-accepted strategy involving grafting short peptide chains to zinc binding groups (ZBG) [6]. Yao and colleagues presented an effective experimental strategy to generate clustered enzymes “fingerprints” through high-throughput screening of focused inhibitors libraries [7]. They have adopted the hydroxamate (CONH-O-) group that chelates strongly to the metal center at the enzyme active site and permuted across the  ,
, 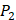 and
and 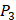 positions, creating a diverse repertoire of 1400 individual inhibitor scaffolds by adopting the split-pool directed sorting synthesis method. In the library, the
positions, creating a diverse repertoire of 1400 individual inhibitor scaffolds by adopting the split-pool directed sorting synthesis method. In the library, the 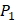 consists of 6 natural amino acids and 5 non-natural amino acids (CPA3, CHG, HPE,
consists of 6 natural amino acids and 5 non-natural amino acids (CPA3, CHG, HPE, 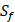 , HSER) [8] (respectively set as single letters of U, B, Z,
, HSER) [8] (respectively set as single letters of U, B, Z,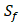 , J), which are made of substituted succinyl hydroxamate ZBG (highlighted in pink) as shown in Scheme 1. The
, J), which are made of substituted succinyl hydroxamate ZBG (highlighted in pink) as shown in Scheme 1. The 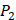 , and
, and 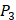 positions respectively consist of 20 natural amino acids. As a result, they reported a data set acquired by seeing a comprehensive panel of 1400 peptide hydroxamates respectively for seven different MMPs, providing unique insights to inhibitor design and preference within this important group of enzymes. However, variation at three positions of hydroxamates peptide can cause differences in binding affinities in total of 4400 possibilities. A large part of binding values of these samples, which can provide nontrivial insights and assistance for inhibitor design, is still missing. Using experimental method to obtain all the missing sequences is expensive, time-consuming and labor-extensive. Hence, we construct a computational model to predict MMP-specific binders from experimental data.
positions respectively consist of 20 natural amino acids. As a result, they reported a data set acquired by seeing a comprehensive panel of 1400 peptide hydroxamates respectively for seven different MMPs, providing unique insights to inhibitor design and preference within this important group of enzymes. However, variation at three positions of hydroxamates peptide can cause differences in binding affinities in total of 4400 possibilities. A large part of binding values of these samples, which can provide nontrivial insights and assistance for inhibitor design, is still missing. Using experimental method to obtain all the missing sequences is expensive, time-consuming and labor-extensive. Hence, we construct a computational model to predict MMP-specific binders from experimental data.
In this paper, we propose the first computational method to identify and analyze MMPs hydroxamates peptides' binding specificity. First, we propose a sampling criteria to construct a training set for each new peptide motif. Then, we select nine physicochemical properties of amino acids, which can effectively describe the differences among amino acids and can also be obtained across non-natural amino acids. We also proposed features of auto-cross covariance [9, 10], extracting correlative properties of amino acids in any two positions. Finally, we adopt random forest to predict binding values of each peptide motif respectively with seven MMPs. On MMP-7, our method has achieved overall Pearson-product-moment correlation (PCC) and root mean squared error (RMSE) values of 0.9181 and 9.3827. The high values of PCC and RMSE of our method on all seven MMPs have proven the rationality and effectiveness of our computational method. In the end, we find 4 novel peptides that selectively bind to MMP-2, including Asp-Ile-Phe, Asp-Ile-Tyr, Asp-Ile-Lys and Hser-Gly-Phe. We also identify 6 novel peptides with high selectivity binding to MMP-7 of Chg-Ile-Ile, Chg-Ile-Leu, Chg-Ile-Glu, Chg-Ile-Met, Chg-Val-Ile and Chg-Val-Leuor, providing instructive insights for further experiment design and detection of highly selective inhibitors of MMPs.
Methods
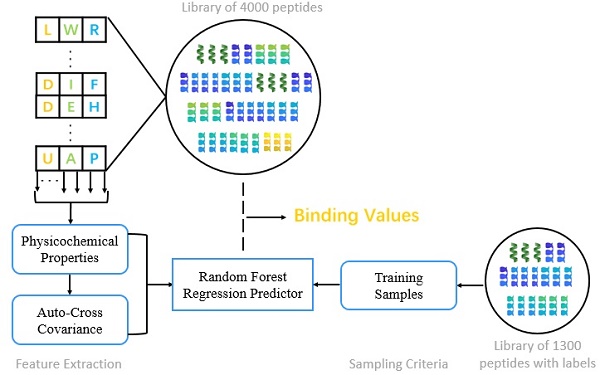
We present the first computational method of MMPs peptide-binding specificity identification. For each MMP, we have 1400 peptide motifs with experimental binding affinity values, treated as known in this study. To identify binding values of 4400 peptide sequences binding to seven MMPs, we firstly propose a sampling criteria to construct an affinity-based training set for each peptide motif. Then we select 9 physicochemical properties of amino acids to describe each peptide motif. We also use auto-cross covariance to extract correlative properties of amino acids in any two positions. Finally, we consider Random Forest to predict affinity values of peptide motifs. The method is shown in Figure 1.
Data set
Yao and co-workers proposed a small but highly diversified 1400-member peptide library [7]. The library was prepared in two parts. First, a 400-member sub-library containing a leucine side chain at 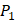 position (represented with single-letter code L) was constructed with permutations of all 20 natural amino acids across
position (represented with single-letter code L) was constructed with permutations of all 20 natural amino acids across 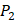 and
and 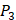 positions. Second, an additional 1000-member set was constructed with the remaining 10 amino acids at
positions. Second, an additional 1000-member set was constructed with the remaining 10 amino acids at 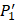 position containing side chains of both natural and non-natural amino acids (Scheme 1). The
position containing side chains of both natural and non-natural amino acids (Scheme 1). The 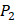 and
and 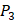 positions in this set were systematically permuted with 10 proteinogenic amino acids, specifically nonpolar (Ala, Leu, Phe, Trp), charged polar (Glu, Lys, His) and uncharged polar (Gln, Ser, Tyr) amino acids. Yao experimented the 1400 peptides and obtained their binding values respectively with seven MMPs to identify selective peptide [7].
positions in this set were systematically permuted with 10 proteinogenic amino acids, specifically nonpolar (Ala, Leu, Phe, Trp), charged polar (Glu, Lys, His) and uncharged polar (Gln, Ser, Tyr) amino acids. Yao experimented the 1400 peptides and obtained their binding values respectively with seven MMPs to identify selective peptide [7].
For each MMP, there are 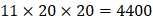 possibilities of inhibitor peptides in total. There could still be a significant number of peptides with high potency and selectivity in the remaining untested 3000 peptides. Hence, we construct a regression model to predict binding values of non-experimental peptides to find effective peptides with high potency and selectivity. For each MMP isoform, we have 1400 peptide motifs with experimental binding affinity values. However, as the physicochemical properties of the amino acid with sulfone side chain (
possibilities of inhibitor peptides in total. There could still be a significant number of peptides with high potency and selectivity in the remaining untested 3000 peptides. Hence, we construct a regression model to predict binding values of non-experimental peptides to find effective peptides with high potency and selectivity. For each MMP isoform, we have 1400 peptide motifs with experimental binding affinity values. However, as the physicochemical properties of the amino acid with sulfone side chain (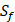 ) are unobtainable, the peptide motifs containing an
) are unobtainable, the peptide motifs containing an 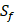 can't be effectively described or further be used as training data. Thus we forgo
can't be effectively described or further be used as training data. Thus we forgo 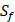 and the peptides with
and the peptides with 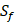 . As a result, we use 1300 peptide motifs as training samples to predict the non-experimental peptides. The non-experimental peptides which can be effectively predicted are also the ones without
. As a result, we use 1300 peptide motifs as training samples to predict the non-experimental peptides. The non-experimental peptides which can be effectively predicted are also the ones without 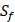 on
on  position. There are, hence,
position. There are, hence, 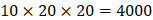 peptides' binding values predicted by our regression model.
peptides' binding values predicted by our regression model.
The optional non-natural and natural amino acids for three positions. The 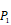 consists of 11 non-natural and natural amino acids made of substituted succinyl hydroxamate ZBG (highlighted in pink). Each was assigned a unique single-letter code (inset).
consists of 11 non-natural and natural amino acids made of substituted succinyl hydroxamate ZBG (highlighted in pink). Each was assigned a unique single-letter code (inset).
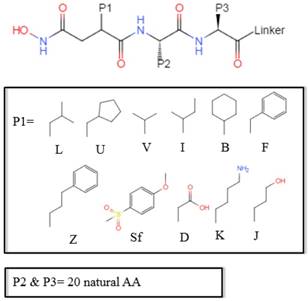
The overall method flow.
Sampling Criteria
We propose a sampling criteria to build a predictor for each new peptide motif. If all 1300 peptide motifs are used to construct a regression model, the predictor would be confused due to importing many irrelevant peptide sequences. Here, we exploit a similarity-based sampling approach. All 20 natural amino acids and 5 non-natural amino acids are divided into 5 categories [11, 12]: amino acids with positive charged side chains, amino acids with negative charged side chains, amino acids with polar uncharged side chains, amino acids with hydrophobic side chains and special cases. The details are shown in Table 1.
Five categories of 20 natural amino acids and 5 non-natural amino acids
| Category | Amino Acids |
|---|---|
| Amino acids with positive charged side chains | R, H, K, B |
| Amino acids with negative charged side chains | D, E, J, Z |
| Amino acids with polar uncharged side chains | S, T, N, Q |
| Amino acids with hydrophobic side chains | A, I, L, M, F, W, Y, V |
| Special cases | C, G, P, U, 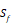 |
We propose an evaluation of similarity between two peptide samples based on the similarity 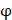 of amino acid categories. We calculate the similarity between the training peptide sample
of amino acid categories. We calculate the similarity between the training peptide sample 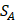 and the target peptide sequence
and the target peptide sequence 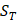 as follows:
as follows:
(1)
where 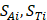 respectively denotes corresponding amino acid on the i-th position of training and target peptide;
respectively denotes corresponding amino acid on the i-th position of training and target peptide; 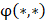 represents the amino acid similarity: if two amino acids belong to the same category, the similarity
represents the amino acid similarity: if two amino acids belong to the same category, the similarity 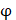 on this position is 1, otherwise is 0.
on this position is 1, otherwise is 0.
For each target sequence motif, we choose samples which have similarity values of at least 1 (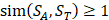 ), which means each sample at least has one position's amino acid belonging to the same category with amino acid on the corresponding position of target peptide. Compared with other random-based sampling approach, the similarity-based sampling strategy takes similarity into consideration and hence filter the irrelevant samples.
), which means each sample at least has one position's amino acid belonging to the same category with amino acid on the corresponding position of target peptide. Compared with other random-based sampling approach, the similarity-based sampling strategy takes similarity into consideration and hence filter the irrelevant samples.
Feature Extraction
The computational methods have been widely used for classifying peptides or predicting binding values of small-molecules containing natural amino acids. [13, 14, 15, 16, 17]. However, there have been challenges employing computational methods to peptides containing non-natural amino acids because it's hard to extract effective features to describe and differentiate non-natural amino acids. We herein propose two kinds of features in this study to effectively describe both non- and natural amino acids: one extracts nine physicochemical properties for each position and this produces 27 features; the other extracts correlation of amino acids in any two positions of auto-cross covariance, nine features for every two positions, thus leads to another 27 features.
Physicochemical Properties
We compute 9 physicochemical properties [18] of all 20 amino acids and 4 non-natural amino acids (B, J, T, U) to describe each peptide motif using E-dragon [19] and MOE programs [20]. The amino acid with sulfone side chain 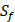 has been omitted, due to its physicochemical properties unable to be computed. These 9 physicochemical properties consist of Molecular Weight (MW), Sum of Atomic Van Der Waals Volumes (SV), Sanderson Electronegativity (SE), Polarizability (P), Number of hydrogen bonds (HB), Eccentric Connectivity Index (CSI), Eccentricity (ECC), Sphericity (SPH), Hydrophilic factor (HY). Details are shown in Table 2. These nine physicochemical properties are normalized to zero mean and unit standard deviation [21, 22, 23]. The first kind of 27 features can be extracted from these normalized properties as follows:
has been omitted, due to its physicochemical properties unable to be computed. These 9 physicochemical properties consist of Molecular Weight (MW), Sum of Atomic Van Der Waals Volumes (SV), Sanderson Electronegativity (SE), Polarizability (P), Number of hydrogen bonds (HB), Eccentric Connectivity Index (CSI), Eccentricity (ECC), Sphericity (SPH), Hydrophilic factor (HY). Details are shown in Table 2. These nine physicochemical properties are normalized to zero mean and unit standard deviation [21, 22, 23]. The first kind of 27 features can be extracted from these normalized properties as follows:
(2)
where 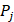 represents the mean of the j-th property,
represents the mean of the j-th property, 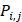 is the j-th property of the i-th amino acid,
is the j-th property of the i-th amino acid, 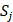 is the corresponding unit standard deviation.
is the corresponding unit standard deviation.
Nine physicochemical properties of 20 natural amino acids and 5 non-natural amino acids.
| AA | MW | SV | SE | P | HB | CSI | ECC | SPH | HY | |
|---|---|---|---|---|---|---|---|---|---|---|
| ALA | A | 90.12 | 7.11 | 14.35 | 7.58 | 2 | 24 | 16 | 0.576 | 3.794 |
| GLY | G | 75.08 | 5.21 | 10.52 | 5.44 | 2 | 19 | 13 | 0.828 | 2.870 |
| IIE | I | 132.21 | 11.90 | 23.00 | 12.86 | 2 | 61 | 37 | 0.557 | 2.926 |
| LEU | L | 132.21 | 11.90 | 23.00 | 12.86 | 2 | 63 | 38 | 0.500 | 2.926 |
| PRO | P | 116.16 | 9.71 | 18.23 | 10.34 | 2 | 51 | 27 | 0.651 | 2.001 |
| VAL | V | 118.18 | 10.31 | 20.12 | 11.10 | 2 | 43 | 27 | 0.410 | 3.150 |
| PHE | F | 166.22 | 14.31 | 24.12 | 15.10 | 2 | 131 | 68 | 0.831 | 2.456 |
| TRP | W | 205.26 | 17.30 | 28.22 | 18.11 | 3 | 195 | 95 | 0.852 | 3.198 |
| TYR | Y | 182.22 | 14.82 | 25.44 | 15.56 | 3 | 157 | 82 | 0.787 | 3.446 |
| ASP | D | 134.13 | 9.13 | 18.00 | 9.49 | 4 | 63 | 38 | 0.708 | 4.320 |
| GLU | E | 148.16 | 10.73 | 20.89 | 11.25 | 4 | 85 | 50 | 0.770 | 4.068 |
| ARG | R | 176.26 | 14.59 | 28.36 | 15.50 | 4 | 139 | 79 | 0.863 | 8.560 |
| HIS | H | 156.19 | 12.10 | 21.55 | 12.59 | 4 | 106 | 55 | 0.644 | 3.857 |
| LYS | K | 148.24 | 13.20 | 26.04 | 14.25 | 2 | 98 | 57 | 0.836 | 6.438 |
| SER | S | 106.12 | 7.62 | 15.68 | 8.03 | 4 | 36 | 23 | 0.652 | 4.875 |
| THR | T | 120.15 | 9.22 | 18.56 | 9.80 | 4 | 43 | 27 | 0.450 | 4.508 |
| CYS | C | 122.19 | 8.20 | 15.43 | 9.23 | 2 | 36 | 23 | 0.668 | 4.875 |
| MET | M | 150.25 | 11.39 | 21.19 | 12.75 | 2 | 74 | 44 | 0.810 | 3.032 |
| ASN | N | 133.15 | 9.62 | 18.78 | 10.04 | 4 | 63 | 38 | 0.734 | 5.574 |
| GLN | Q | 147.18 | 11.21 | 21.66 | 11.80 | 4 | 85 | 50 | 0.787 | 5.271 |
| CHG | B | 158.25 | 14.50 | 26.88 | 15.63 | 2 | 101 | 53 | 0.477 | 2.587 |
| HSER | J | 120.15 | 9.22 | 18.56 | 9.80 | 4 | 54 | 33 | 0.735 | 4.508 |
| HPE | Z | 180.25 | 15.90 | 27.00 | 16.86 | 2 | 163 | 84 | 0.762 | 2.342 |
| CPA3 | U | 157.24 | 14.20 | 25.94 | 15.24 | 2 | 106 | 55 | 0.595 | 1.574 |
MW, Molecular Weight; SV, Sum of Atomic Van Der Waals Volumes; SE, Sanderson Electronegativity; P, Polarizability; HB, Number of hydrogen bonds; CSI, Connectivity Index; ECC, Eccentricity; SPH, Sphericity; HY, Hydrophilic factor.
Auto-Cross Covariance
We also use auto-cross covariance to extract correlation of amino acids in any two positions. Auto-cross covariance (ACC) can get two kinds of variables, auto cross (AC) between the same descriptor, and cross covariance (CC) between two different descriptors. In this study, we only use AC variables in order to avoid generating too large number of variants. We modify the AC variables to get correlation of amino acids in any two positions as follows:
(3)
where m, n are different position of a peptide and j is the j-th property of residues, 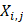 is the j-th property of residue on the i-th position.
is the j-th property of residue on the i-th position.
Random Forest
The training algorithm for random forest [24, 25, 26] applies the general technique of bagging. Given a training set of 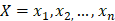 with responses
with responses 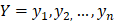 , bagging repeatedly and randomly selects a sample for B times with replacement of the training set and fits trees to these samples:
, bagging repeatedly and randomly selects a sample for B times with replacement of the training set and fits trees to these samples:
For b = 1, 2, …, B:
- Sample, with replacement, n training examples from X, Y; call these
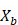 ,
, 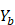 .
. - Train a regression tree
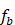 on
on 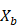 ,
, 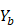 .
.
After training, predictions for unseen samples 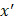 can be obtained by averaging the predictions from all the individual regression trees on
can be obtained by averaging the predictions from all the individual regression trees on 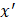 :
:
(4)
We calculate a five-fold cross-validation and permute from 100 to 5000 with step of 1 to get the optimal number of regression trees for random forest regression model. We create an ensemble of 1500 regression trees for predicting non-experimental peptides' binding values.
Results
The 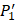 position contains 5 non-natural amino acids, one of which has a side chain of sulfone (
position contains 5 non-natural amino acids, one of which has a side chain of sulfone (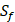 ). Among the 1400 experimented samples, there are 10 x 10= 100 peptides with
). Among the 1400 experimented samples, there are 10 x 10= 100 peptides with 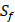 on
on 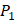 position and 10 proteinogenic amino acids permuted on
position and 10 proteinogenic amino acids permuted on 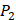 and
and 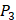 positions. Among the 4400 peptides totally in the library, there are 20 x 20 =400 peptides with
positions. Among the 4400 peptides totally in the library, there are 20 x 20 =400 peptides with 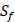 on
on 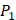 position and 20 natural amino acids permuted on
position and 20 natural amino acids permuted on 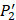 and
and 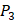 positions. Due to the physicochemical properties of
positions. Due to the physicochemical properties of 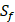 , the total number of experimental samples which can be used is 1300; the total number of sequences which regression model can predict is 4000. In this section, we complete three kinds of experiments. First, our method verifies on the 1300 known peptide motifs binding to seven distinct but highly homologous MMPs. Second, our method tests on 4000 peptide sequences to predict binding affinity values. Third, we identify peptides that preferentially bind to MMP-2 and MMP-7 over other MMPs.
, the total number of experimental samples which can be used is 1300; the total number of sequences which regression model can predict is 4000. In this section, we complete three kinds of experiments. First, our method verifies on the 1300 known peptide motifs binding to seven distinct but highly homologous MMPs. Second, our method tests on 4000 peptide sequences to predict binding affinity values. Third, we identify peptides that preferentially bind to MMP-2 and MMP-7 over other MMPs.
Effectiveness of the regression model
To test the effectiveness of our method, we verify 1300 peptide motifs binding to seven MMPs respectively with Leave-one-out validation and two-fold cross-validation (to avoid overfitting) combining with 1500-tree random forest regression model. The Pearson-product-moment correlation coefficient (PCC) and the root mean squared error (RMSE) are used to evaluate performance:
(5)
(6)
where D contains all relevant binding motifs, 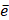 is the average binding affinity,
is the average binding affinity, 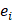 denotes experimental binding affinity value of the i-th peptide sequence,
denotes experimental binding affinity value of the i-th peptide sequence, 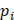 denotes the predicted affinity value of the i-th peptide sequence. An accurate predictor will get PCC=1, RMSE=0.
denotes the predicted affinity value of the i-th peptide sequence. An accurate predictor will get PCC=1, RMSE=0.
When employing Leave-one-out Validation, for each predicted peptide, we use 1299 peptide motifs with experimental binding affinity values as training data, removing the predicted one. When adopting the two-fold cross validation, we split the 1300 peptide motifs into two folds. We respectively use each fold as training set and the other fold as validation set. The validation results of identifying peptide motifs binding to MMPs are shown in Table 3. On all the seven MMPs isoform, our method achieved significant PCC and RMSE. The performance of 2-fold cross-validation is slightly lower than leave-one-out validation, but it is still satisfactory and can prove the effectiveness of our regression model.
Effectiveness of the Sampling Criteria
When adopting the sampling criteria, we only select relevant samples for building the predictor. The average number of relevant samples for each peptide motif is 1069, which means, for each predicted peptide, we use around 1069 samples as training set. Around 230 samples on average are irrelevant samples and were excluded by the sampling criteria. To test the effectiveness of the Sampling Criteria, we verify the 1300 peptide motifs binding to seven MMPs with 1500-tree random forest regression model respectively trained with the relevant samples and irrelevant samples. The validation results are shown in Table 4, which shows the effectiveness of our sampling criteria.
Comparison to Computational Methods
In this study, we use Random Forest as regression model, which gets a better result and costs less time compared with other techniques. The quantitative comparison with other techniques, such as Neural Network with one hidden layer and 100 nets, Lasso Regression, Kernel Ridge Regression are as shown in Table 5.
On the MMP-2 isoform, Random Forest has achieved overall PCC and RMSE values of 0.8212 and 17.7916; Lasso Regression has PCC and RMSE values of 0.5547 and 25.9458; Ridge Regression with Gaussian Kernel has PCC and RMSE values of 0.7240 and 21.5097; Neural Network with one hidden layer has RMSE values of 33.6099. For seven MMPs, our method using Random Forest outperformed other excellent regression techniques.
Comparison to Experimental Methods
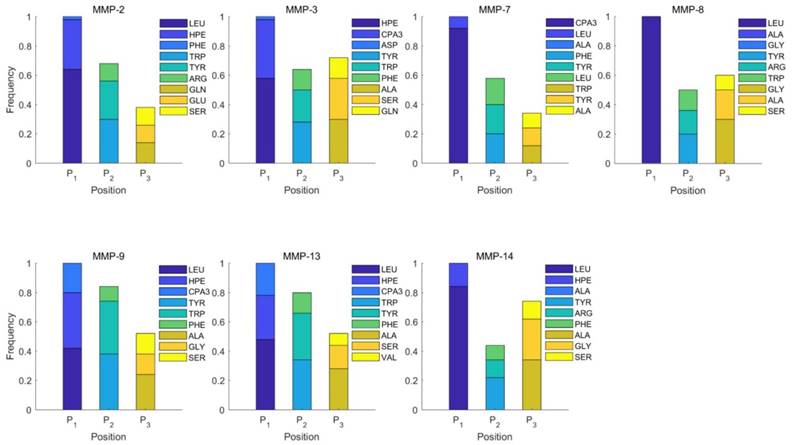
We produce a position-specific scoring histogram [27] among the top 50 binding-value motifs against each individual MMP isoform to reflect specialty for each position as shown in Figure 2. For each MMP protein, we select its binding peptides with top 50 binding values predicted by our regression model. Then we analyze the frequency of appearance of each amino acid on each position among the top 50 predicted peptides of the specific MMP. The x axis denotes nominal positions of a binding peptide from 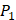 to
to 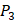 . The y axis and the height of a letter denotes its frequency of appearance on this position, implicating its contribution of binding value to the position. From the 1300 samples, for peptides binding adherently with MMP-2,
. The y axis and the height of a letter denotes its frequency of appearance on this position, implicating its contribution of binding value to the position. From the 1300 samples, for peptides binding adherently with MMP-2, 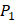 Tyrically has conservative amino acids of Leu and Hpe (amino acid with an aromatic side chain of long-Phe),
Tyrically has conservative amino acids of Leu and Hpe (amino acid with an aromatic side chain of long-Phe), 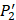 is Tyrical of amino acid Trp; for peptides binding adherently with MMP-7,
is Tyrical of amino acid Trp; for peptides binding adherently with MMP-7, 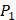 Tyrically has a conservative amino acid of CPA3 with a unique hydrophobic side chain. Actually, as we can see from Figure 2, peptide motifs with Leu on
Tyrically has a conservative amino acid of CPA3 with a unique hydrophobic side chain. Actually, as we can see from Figure 2, peptide motifs with Leu on 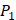 position are conservatively with the high binding values with all seven MMPs, which conforms the significant pattern that inhibitors with high potency against MMPs family are highly homogenous.
position are conservatively with the high binding values with all seven MMPs, which conforms the significant pattern that inhibitors with high potency against MMPs family are highly homogenous.
In order to better visualize more detailed contributions of different positions, potencies from each of the 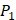 ,
, 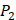 ,
, 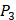 side chains in the inhibitor library are averaged and graphically presented in Figure 3. Each picture represents one position of a MMP isoform. The y-axis denotes the average binding values of peptides which have the specific amino acid Tyre on this position. The x-axis denotes the appearance of amino acid Tyre on this position. We select the top 10 amino acids with highest mean binding values on
side chains in the inhibitor library are averaged and graphically presented in Figure 3. Each picture represents one position of a MMP isoform. The y-axis denotes the average binding values of peptides which have the specific amino acid Tyre on this position. The x-axis denotes the appearance of amino acid Tyre on this position. We select the top 10 amino acids with highest mean binding values on 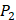 and
and 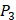 positions. We have identified top 3 amino acids with highest mean binding values on each position as shown in Table 6.
positions. We have identified top 3 amino acids with highest mean binding values on each position as shown in Table 6.
Our method is compared with the experimental method of Yao [7]. They also identified amino acids with highest averaged binding values as shown in Table 6. On 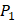 position, they averaged all 1400 peptides to get 11 mean values of each amino acid Tyre. However, on
position, they averaged all 1400 peptides to get 11 mean values of each amino acid Tyre. However, on 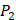 and
and 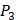 positions, they only averaged binding values of the 10 kinds of amino acids, which has permutated across 11 kinds on
positions, they only averaged binding values of the 10 kinds of amino acids, which has permutated across 11 kinds on 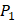 . So they got values of a relatively similar trend across 10 kinds of amino acids respectively within
. So they got values of a relatively similar trend across 10 kinds of amino acids respectively within 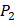 and
and 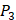 . We averaged all 24 kinds of amino acids of 1400 samples in Figure 3. And as shown in Figure 3 and Table 6, on
. We averaged all 24 kinds of amino acids of 1400 samples in Figure 3. And as shown in Figure 3 and Table 6, on 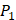 position, our computational results are consistent with the previous experimental works on MMPs binding peptide motifs, proving the reliability of our method. On
position, our computational results are consistent with the previous experimental works on MMPs binding peptide motifs, proving the reliability of our method. On 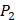 and
and 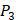 positions, our mean values of the 10 kinds of amino acids (Ala, Leu, Phe, Trp, Glu, Lys, His, Gln, Ser, Tyr) are consistent with experimental method, although some of which are omitted from Figure 3, due to their relatively low mean values. Our computational results also show that Gly is also a conservative amino acid on
positions, our mean values of the 10 kinds of amino acids (Ala, Leu, Phe, Trp, Glu, Lys, His, Gln, Ser, Tyr) are consistent with experimental method, although some of which are omitted from Figure 3, due to their relatively low mean values. Our computational results also show that Gly is also a conservative amino acid on 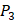 when Leu on
when Leu on 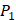 position.
position.
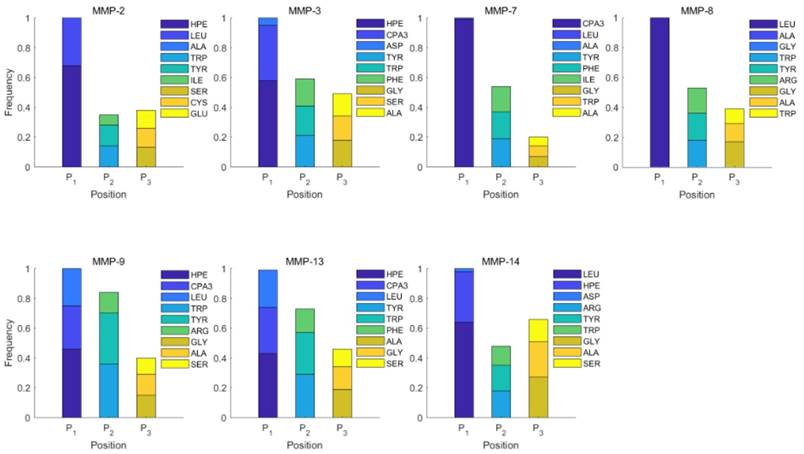
Prediction on 4000 peptide sequences
In the predicted library of 4000 peptides, we produce a position-specific scoring histogram among the top 100 binding-values motifs against each individual MMP isoform to reflect specialty for each position as shown in Figure 4. For each MMP protein, we select its binding peptides with top 100 binding values predicted by our regression model. Then we analyze the frequency of appearance of each amino acid on each position among the top 100 predicted peptides of the specific MMP. From the 4000 samples, for peptides binding adherently with MMP-2, 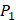 Tyrically has conservative amino acids of Leu and Hpe, which is consistent with analyze result of 1300 samples; for peptides binding adherently with MMP-7,
Tyrically has conservative amino acids of Leu and Hpe, which is consistent with analyze result of 1300 samples; for peptides binding adherently with MMP-7, 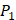 Tyrically has a conservative amino acid of Leu. Our predicted result of 4000 sequences manifests peptides with Hpe and Leu amino acids on
Tyrically has a conservative amino acid of Leu. Our predicted result of 4000 sequences manifests peptides with Hpe and Leu amino acids on 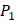 conservatively have high binding values with seven MMPs. However, these peptides can't be used as inhibitors as they will also inhibit beneficial MMPs. So in the next part we will identify peptides with high selectivity.
conservatively have high binding values with seven MMPs. However, these peptides can't be used as inhibitors as they will also inhibit beneficial MMPs. So in the next part we will identify peptides with high selectivity.
Specificity of MMP-2 and MMP-7 binding peptide motifs
From the analysis of Figure 4, we can only identify which amino acid Tyre on each position has the highest potency against the MMP isoform, which are highly conserved. What would really benefit us is to identify peptides with not only high potency but also high selectivity, which bind coherently against specific MMPs, namely MMP-2 and MMP-7, while showing little binding values against other MMPs. So from the 4000 peptide motifs binding values results predicted by our computational method, we respectively identify peptides with selectivity to bind MMP-2 and MMP-7.
Validation on 1300 peptide motifs using random forest with 1500 trees.
| Leave-One-Out Validation | Two-fold Cross-Validation | |||
|---|---|---|---|---|
| PCC | RMSE | PCC | RMSE | |
| MMP-2 | 0.8212 | 17.7916 | 0.7836 | 19.3735 |
| MMP-3 | 0.7682 | 17.2379 | 0.7117 | 18.9166 |
| MMP-7 | 0.9181 | 9.3827 | 0.9053 | 10.0559 |
| MMP-8 | 0.8910 | 12.4845 | 0.8756 | 13.2831 |
| MMP-9 | 0.9124 | 12.0189 | 0.8893 | 13.4283 |
| MMP-13 | 0.8708 | 16.2411 | 0.8448 | 17.6808 |
| MMP-14 | 0.7247 | 16.7657 | 0.6910 | 17.5881 |
Validation on 1300 peptide motifs using random forest with 1500 trees with Sampling Criteria.
| Training Set with Relevant Samples | Training Set with Irrelevant Samples | ||
|---|---|---|---|
| PCC | RMSE | RMSE | |
| MMP-2 | 0.8195 | 17.8608 | 35.1576 |
| MMP-3 | 0.7680 | 17.2457 | 29.8699 |
| MMP-7 | 0.9181 | 9.3803 | 29.5143 |
| MMP-8 | 0.8908 | 12.4952 | 33.2383 |
| MMP-9 | 0.9095 | 12.2094 | 37.6389 |
| MMP-13 | 0.8680 | 16.4052 | 44.0620 |
| MMP-14 | 0.7246 | 16.7671 | 25.9060 |
Validation of binding values of inhibitors of MMP-2 with distinct computational methods.
| PCC | RMSE | |
|---|---|---|
| Lasso Regression | 0.5547 | 25.9458 |
| Neural Network | - | 33.6099 |
| Ridge Regression with Gaussian Kernel | 0.7240 | 21.5097 |
| Random Forest | 0.8212 | 17.7916 |
Comparison with Experimental method of top average binding values on 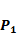 position
position
| Yao | Ours | |
|---|---|---|
| MMP-2 | Z | Z |
| MMP-3 | Sf, U, Z | U, Z |
| MMP-7 | U | U |
| MMP-8 | Z, L | Z |
| MMP-9 | Z | Z |
| MMP-13 | Z | Z |
| MMP-14 | L | L |
Position-specific scoring histogram on top 50 binding-value motifs of 1300 samples against seven MMPs. For each MMP protein, we select its binding peptides with top 50 predicted binding values among 1300 library. Each bar represents the frequency of appearance of each amino acid Tyre on each position among the top 50 predicted binding peptides of the specific MMP. The x axis denotes nominal positions of a binding peptide from 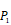 to
to 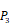 . The y axis and the height of a letter denotes its frequency of appearance on this position, implicating its contribution of binding value to the position.
. The y axis and the height of a letter denotes its frequency of appearance on this position, implicating its contribution of binding value to the position.
Averaged inhibition contributions across permuted 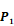 ,
, 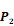 and
and 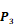 positions. Each bar represents averaged inhibition values of relevant residue across 1300-member library. The asterisk (*) highlights the residue contributing to the highest inhibition average in each graph.
positions. Each bar represents averaged inhibition values of relevant residue across 1300-member library. The asterisk (*) highlights the residue contributing to the highest inhibition average in each graph.
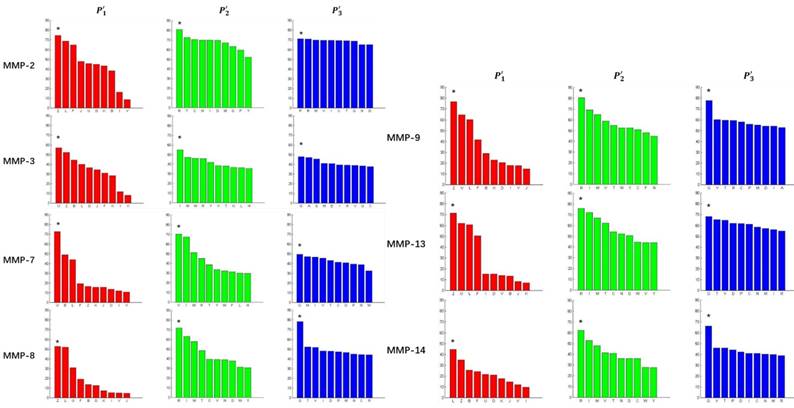
We filter peptides with high selectivity of MMP-2, which have binding values with MMP-2 higher than 60, and have binding values with other MMPs less than 20. We successfully obtain 5 inhibitor candidates of Asp-Ile-Phe, Asp-Ile-Tyr, Asp-Ile-Lys and Hser-Gly-Phe as shown in Table 7. Detailed binding values are shown in Table 8. We also filter peptides with high selectivity of MMP-7, which have binding values with MMP-7 higher than 60, and have binding values with other MMPs less than 30. We successfully obtain 6 inhibitor candidates of Chg-Ile-Ile, Chg-Ile-Leu, Chg-Ile-Glu, Chg-Ile-Met, Chg-Val-Ile and Chg-Val-Leu as shown in Table 7. Detailed binding values are shown in Table 9.
From the inhibitors with high selectivity of MMP-2 we find, only one peptide, Hser-Leu-His, labeled with an asterisk (*), is identified in the experimental method. Our computational method finds 4 novel peptides with high selectivity toward MMP-2, and 6 novel peptides with high selectivity toward MMP-7, a known target in pancreatic cancer and intestinal adenoma. As we can see in Table 7, our results of inhibitor candidates of MMP-2 confirms the conclusion of experimental methods that  side chains containing Asp (D) and Hser (J) were found as inhibitors with strong selectivity to perturb MMP-2 [7]. For peptides with high selectivity toward MMP-7, Chg amino acid on
side chains containing Asp (D) and Hser (J) were found as inhibitors with strong selectivity to perturb MMP-2 [7]. For peptides with high selectivity toward MMP-7, Chg amino acid on  position showed strong selectivity. On
position showed strong selectivity. On  position, Val and Ile, which both have hydrophobic side chains of alkyls, also showed preference to bind to MMP-7. Our findings, which although is by no means exhaustive, facilitated the identification of inhibitors with good potency as well as desirable selectivity, providing significant insights of candidate inhibitor drugs.
position, Val and Ile, which both have hydrophobic side chains of alkyls, also showed preference to bind to MMP-7. Our findings, which although is by no means exhaustive, facilitated the identification of inhibitors with good potency as well as desirable selectivity, providing significant insights of candidate inhibitor drugs.
Inhibitors predicted by computational method with high potency and selectivity with MMP-2 and MMP-7
| No. | MMP-2 | MMP-7 |
|---|---|---|
| 1 | HSER-LEU-HIS * | CHG-ILE-ILE |
| 2 | ASP-ILE-PHE | CHG-ILE-LEU |
| 3 | ASP-ILE-TYR | CHG-ILE-GLU |
| 4 | ASP-ILE-LYS | CHG-ILE-MET |
| 5 | HSER-GLY-PHE | CHG-VAL-ILE |
| 6 | CHG-VAL-LEU |
The binding values against MMPs of inhibitors with high selectivity of MMP-2 predicted by computational method
| MMP-2 | MMP-3 | MMP-7 | MMP-8 | MMP-9 | MMP-13 | MMP-14 | |
|---|---|---|---|---|---|---|---|
| Hser-Leu-His | 60.5067 | 19.7844 | 16.7174 | 1.22158 | 9.5357 | 1.6049 | 8.3165 |
| Asp-Ile-Phe | 65.9515 | 16.5326 | 18.1990 | 0.39054 | 15.2081 | 1.7737 | 11.3050 |
| Asp-Ile-Tyr | 66.5144 | 18.0813 | 17.9488 | 0.10264 | 15.7835 | 0.9748 | 8.8563 |
| Asp-Ile-Lys | 61.4983 | 14.9883 | 17.0719 | 0.51577 | 10.3562 | 3.1173 | 14.9769 |
| Hser-Gly-Phe | 64.4088 | 17.8065 | 16.4288 | 2.24950 | 13.1266 | 5.9196 | 13.8823 |
The binding values against MMPs of inhibitors with high selectivity of MMP-7 predicted by computational method
| MMP-2 | MMP-3 | MMP-7 | MMP-8 | MMP-9 | MMP-13 | MMP-14 | |
|---|---|---|---|---|---|---|---|
| Chg-Ile-Ile | 24.7546 | 21.6090 | 64.3935 | 8.0101 | 24.6581 | 21.9287 | 24.5430 |
| Chg-Ile-Leu | 19.2488 | 18.2610 | 62.8014 | 6.1657 | 24.1854 | 24.0525 | 22.9100 |
| Chg-Ile-Glu | 63.9129 | 27.2415 | 60.7542 | 18.0563 | 17.8181 | 2.32008 | 25.0958 |
| Chg-Ile-Met | 48.4514 | 29.6585 | 63.2750 | 15.3248 | 21.0132 | 11.3537 | 22.0503 |
| Chg-Val-Ile | 22.8662 | 24.8929 | 61.1206 | 7.2634 | 19.4140 | 19.4965 | 21.4045 |
| Chg-Val-Leu | 18.8152 | 23.2073 | 60.0980 | 5.5433 | 18.4461 | 21.3667 | 19.1914 |
Position-specific scoring histogram on top 100 binding-value motifs of 4000 samples against seven MMPs. For each MMP protein, we select its binding peptides with top 100 predicted binding values among 4000 library. Each bar represents the frequency of appearance of each amino acid Tyre on each position among the top 100 predicted binding peptides of the specific MMP. The x axis denotes nominal positions of a binding peptide from 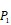 to
to 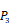 . The y axis and the height of a letter denotes its frequency of appearance on this position, implicating its contribution of binding value to the position.
. The y axis and the height of a letter denotes its frequency of appearance on this position, implicating its contribution of binding value to the position.
Future Work
From the predicted binding values of our computational method, we identify 4 novel peptides with high selectivity toward MMP-2 of Asp-Ile-Phe, Asp-Ile-Tyr, Asp-Ile-Lys and Hser-Gly-Phe. We also identify 6 novel peptides with high selectivity toward MMP-7 of Chg-Ile-Ile, Chg-Ile-Leu, Chg-Ile-Glu, Chg-Ile-Met, Chg-Val-Ile and Chg-Val-Leu. Future work will be done to experimentally test the real binding values of these 10 inhibitors to verify its potency and selectivity.
Abbreviations
MMPs: matrix metalloproteases; PCC: pearson-product-moment correlation coefficient; RMSE: root mean squared error; ZBG: zinc binding groups; MW: molecular weight; SV: sum of atomic van der waals Volumes; SE: Sanderson electronegativity; P: polarizability; HB: number of hydrogen bonds; CSI: connectivity index; ECC: eccentricity; SPH: sphericity; HY: hydrophilic factor; ACC: auto-cross covariance.
Acknowledgements
This research and this article's publication expenditures are supported by a grant from the National Science Foundation of China (NSFC 61772362) and the Tianjin Research Program of Application Foundation and Advanced Technology (16JCQNJC00200)
Author Contributions
All of the authors listed made substantial contributions to the manuscript and qualify for authorship, and no authors have been omitted. Conception and design: Jian Song, Fei Guo; analysis and interpretation of data: Jian Song, Fei Guo; writing and revision of the manuscript: Jian Song, Fei Guo.
Competing Interests
The authors have declared that no competing interest exists.
References
1. Overall C M, Kleifeld O. Validating matrix metalloproteinases as drug targets and anti-targets for cancer therapy. Nature Reviews Cancer. 2006;6(3):227-239
2. Chen W, Ding H, Feng P. et al. iACP: a sequence-based tool for identifying anticancer peptides. Oncotarget. 2016;7(13):16895
3. Overall C M, Kleifeld O. Towards third generation matrix metalloproteinase inhibitors for cancer therapy. British journal of cancer. 2006;94(7):941-946
4. Overall C M, Kleifeld O. Towards third generation matrix metalloproteinase inhibitors for cancer therapy. British journal of cancer. 2006;94(7):941-946
5. Cuniasse P, Devel L, Makaritis A. et al. Future challenges facing the development of specific active-site-directed synthetic inhibitors of MMPs. Biochimie. 2005;87(3):393-4020
6. Rao B G. Recent developments in the design of specific matrix metalloproteinase inhibitors aided by structural and computational studies. Current pharmaceutical design. 2005;11(3):295-322
7. Uttamchandani M, Wang J, Li J. et al. Inhibitor fingerprinting of matrix metalloproteases using a combinatorial peptide hydroxamate library. Journal of the American Chemical Society. 2007;129(25):7848-7858
8. Gfeller D, Michielin O, Zoete V. SwissSidechain: a molecular and structural database of non-natural sidechains. Nucleic acids research. 2012;41(D1):D327-D332
9. Guo Y, Yu L, Wen Z. et al. Using support vector machine combined with auto covariance to predict protein-protein interactions from protein sequences. Nucleic acids research. 2008;36(9):3025-3030
10. Mathura V S, Kolippakkam D. APDbase: Amino acid physicochemical properties database. Bioinformation. 2005;1(1):2
11. Wagner I, Musso H. New naturally occurring amino acids. Angewandte Chemie International Edition. 1983;22(11):816-828
12. Feng P, Ding H, Lin H. et al. AOD: the antioxidant protein database. Scientific reports. 2017;7(1):7449
13. Li Z, Tang J, Guo F. Identification of 14-3-3 proteins phosphopeptide-binding specificity using an affinity-based computational approach. PloS one. 2016;11(2):e0147467
14. Li Z, Tang J, Guo F. Learning from real imbalanced data of 14-3-3 proteins binding specificity. Neurocomputing. 2016;217:83-91
15. Wei L, Tang J, Zou Q. SkipCPP-Pred: an improved and promising sequence-based predictor for predicting cell-penetrating peptides. BMC genomics. 2017;18(7):1
16. Tang H, Zou P, Zhang C. et al. Identification of apolipoprotein using feature selection technique. Scientific reports. 2016:6
17. Lai H Y, Chen X X, Chen W. et al. Sequence-based predictive modeling to identify cancerlectins. Oncotarget. 2017;8(17):28169
18. Zeng X, Liao Y, Liu Y. et al. Prediction and validation of disease genes using HeteSim Scores. IEEE/ACM transactions on computational biology and bioinformatics. 2017;14(3):687-695
19. Tetko I V, Gasteiger J, Todeschini R. et al. Virtual computational chemistry laboratory-design and description. Journal of computer-aided molecular design. 2005;19(6):453-463
20. Cheng G, Li G, Xue H. et al. Zwitterionic carboxybetaine polymer surfaces and their resistance to long-term biofilm formation. Biomaterials. 2009;30(28):5234-5240
21. Guo Y, Yu L, Wen Z. et al. Using support vector machine combined with auto covariance to predict protein-protein interactions from protein sequences. Nucleic acids research. 2008;36(9):3025-3030
22. You Z H, Lei Y K, Zhu L. et al. Prediction of protein-protein interactions from amino acid sequences with ensemble extreme learning machines and principal component analysis. BMC bioinformatics. 2013;14(8):S10
23. Su W, Liao X, Lu Y. et al. Multiple Sequence Alignment Based on a Suffix Tree and Center-Star Strategy: A Linear Method for Multiple Nucleotide Sequence Alignment on Spark Parallel Framework. Journal of Computational Biology. 2017
24. Aslam J A, Popa R A, Rivest R L. On Estimating the Size and Confidence of a Statistical Audit. EVT. 2007;7:8
25. Wei L, Xing P W, Su R. et al. CPPred-RF: a sequence-based predictor for identifying cell-penetrating peptides and their uptake efficiency. Journal of Proteome Research. 2017;16(5):2044-2053
26. Sahu A, Runger G, Apley D. Image denoising with a multi-phase kernel principal component approach and an ensemble version. IEEE Applied Imagery Pattern Recognition Workshop. 2011:1-7
27. Crooks G E, Hon G, Chandonia J M. et al. WebLogo: a sequence logo generator. Genome research. 2004;14(6):1188-1190
Author contact
![]() Corresponding author: Fei Guo: fguoedu.cn
Corresponding author: Fei Guo: fguoedu.cn

 Global reach, higher impact
Global reach, higher impact