Impact Factor
ISSN: 1449-2288
Int J Biol Sci 2013; 9(7):702-706. doi:10.7150/ijbs.6473 This issue Cite
Short Research Communication
Nano-mechanical Compliance of Müller Cells Investigated by Atomic Force Microscopy
1. Department of Physics, Texas Tech University, Box 41051, Lubbock, TX 79409, USA.
2. School of Mechanical Engineering, Kyungpook National University, Daegu, South Korea.
Received 2013-4-15; Accepted 2013-7-11; Published 2013-7-20
Abstract
It has been known that a single Müller cell displays a large variation in the cytoskeletal compositions along its cell body, suggesting different mechanical properties in different segments. Müller cells are thought to be involved in many retinal diseases such as retinoschisis, which can be facilitated by a mechanical stress. Thus, mapping of mechanical properties on localized nano-domains of Müller cells could provide essential information for understanding their structural functions in the retina and roles in their pathological progresses. Using Atomic Force Microscopy (AFM) - based bio-nano-mechanics, we have investigated the local variations of the mechanical properties of Müller cells in vitro. We have a particular interest in identifying elastic moduli in regions closer to three distinctive segments of the cells - process, endfoot, and soma. Using the modified spherical AFM probes, we were able to accurately determine mechanical properties, i.e., elastic moduli from the obtained force-distance curves. We found that the regions closer to soma were mechanically more compliant than regions closer to endfoot and process of Müller cells. We found that this lateral heterogeneity of the mechanical compliance within a single Müller cell is consistent with reports from other cell types. The local variation in mechanical compliances along a single Müller cell may support their diverse mechanical functions in the retina such as a soft mechanical embedding, mechanosensing, and neurotrophic functions for neurons.
Keywords: Atomic force microscopy, glial cells, nano-indentation, Young's modulus, mechanical compliance.
Introduction
The retina is made of several cellular layers, composed of several types of neurons and glial cells. Glia, the non-neuronal cell types in the central nervous system, are considered to provide neurons with the supportive function, with the mechanical buffering from trauma, or with the soft embedding for the neurite growth (1). Müller cells are radial glial cells spanning the entire retinal thickness (2). They have an extended funnel shape, and are oriented along the direction of the light propagation. Along a single Müller cell, the cytoskeletal composition is known to largely vary, suggesting different mechanical properties in different segments (3-5). Müller cells are thought to be involved in many retinal diseases such as retinoschisis, which can be facilitated by a mechanical stress (6, 7). Nevertheless, the current research on Müller cells has been vastly focused on their electrophysiological and biochemical properties (8-10). Only a few studies have reported their mechanical properties (11, 12).
Over the last decade, there has been an enormous progress in cellular bio-mechanical research (13-15). Many techniques such as optical tweezers, micropipette aspiration, and magnetic twisting cytometry were developed to quantitatively assess mechanical properties of a single cell. Among these techniques, atomic force microscopy (AFM) - based biomechanics gained a special attention. Unlike global measurement techniques, the AFM as a nano-indenter is capable of measuring mechanical properties from localized nano-domains within a single cell with a nano-meter lateral resolution in liquid environment (16). Although the conventional nano-indentation with AFM suffers from a high stress produced by a sharp AFM tip, we have achieved a remedy for this issue by using a modified spherical tip with a controlled non-destructive stress (100 Pa - 10 kPa) (17).
In this paper, in order to elevate the understanding of physiological and mechanical function of Müller cells, we investigate the local variation of mechanical properties, i.e., elastic moduli of Müller cells using AFM biomechanics. The AFM nano-indentation experiments were performed for the endfeet, soma, and processes of Müller cells as shown in Fig. 1. The standard Hertz model was applied to calculate the elastic moduli from the force-distance (f-d) curves obtained from nano-indentation experiments (18).
One measurement point was selected from each morphologically different region of a single cell. It is not feasible to obtain AFM topographic images of a whole cell with a reasonable scanning stress because Müller cells usually did not develop robust adhesion to a hard glass substrate, and the thickness measured from the hard substrate to apical membrane was beyond the vertical range of the AFM scanner (7.5 μm). Thus, before taking f-d curves, we identified measurement points by obtaining the AFM topographic images only near the apical membrane of cells with a minimal scanning stress in order to prevent cells from disengaging from the substrate.
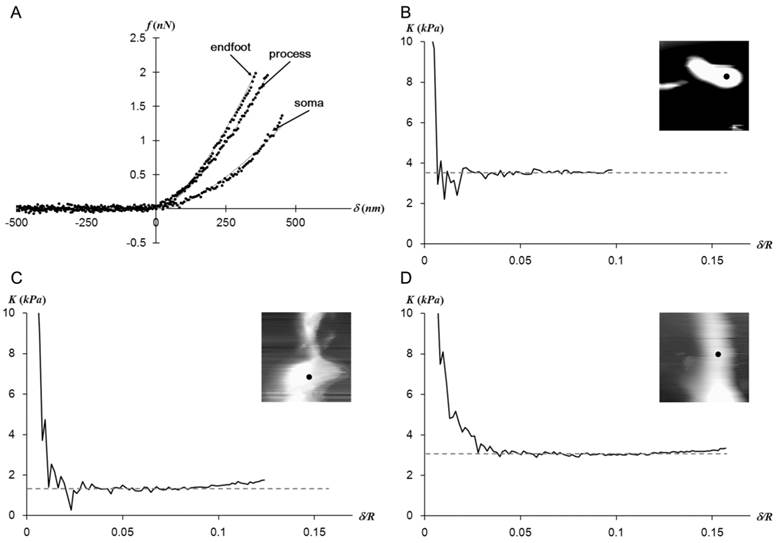
The Hertz model fits well with the f-d curves regardless of the measurement regions as shown in Fig. 2A. The plateaus of the elastic constant K vs. δ/R in Fig. 2B-D imply that Müller cells display a mechanically linear and homogeneous behavior within the observed stress range.
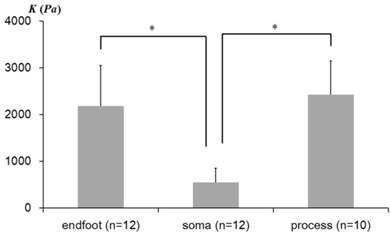
The average elastic constants K determined from three distinctive regions of Müller cells are shown in Fig. 3. The statistical analyses were performed to determine whether the elastic constants vary in different morphological regions of Müller cells. As plotted in Fig. 3, the elastic constant K in the regions closer to the soma (Avg ± Stdev = 546 ± 311 Pa, n = 12) were significantly lower than those in the regions closer to the endfoot (2,185 ± 866 Pa, n = 12) (p = 2.59 × 10-5) and the distal process (2,423 ± 722 Pa, n = 10) (p= 9.18 × 10-4). However, the endfoot and the distal process did not display a statistically meaningful difference from each other. Thus, from the statistical analyses of the elastic constants determined from the local domains of Müller cells, we found that Müller cells are mechanically heterogeneous in the lateral direction, although they seem to display a mechanical homogeneity in the vertical direction (see the plateau of Fig. 2B-D).
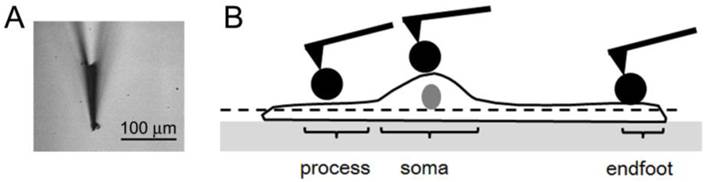
(a) The bright field optical image of a modified AFM probe using the spherical polystyrene beads. (b) The schematic description of where AFM force-distance (f-d) curves were obtained from a Müller cell. The f-d curves were obtained from the process, soma, endfoot of a single Müller cell after obtaining a topographic image on the apical surface of each region. The dashed line represents that the scanning force was limited to the apical surface.
(a) The representative f-d extension curves obtained from points closer to three different regions of a Müller cell. The obtained data (dots) fit well with the Hertz model (solid lines).While the f-d curves obtained from the endfoot and process resemble each other, the one obtained from the soma deviates from other curves. The elastic constant (K) - indentation (δ) curves corresponding to data presented in (a) were presented in (b) for endfoot, (c) for soma, and (d) for process. The insets are the AFM deflection images (25 μm × 25 μm) obtained from the AFM contact mode imaging from each region. The f-d curve measurement point was shown as a dot in the inset. The plateau of K implies a mechanically linear and homogeneous behavior of Müller cells in the vertical direction.
The average elastic constants measured from regions closer to the endfoot, soma, and process. The error bar represents the standard deviation (* p<0.01). n represents the number of the AFM indentation experiments from multiple cells.
The lateral heterogeneity of mechanical compliance, i.e., elastic moduli observed in Müller cells is consistent with the previous reports (11, 17, 19). Due to the compositional difference in the cytoskeletal organization in local regions of a Müller cell, the regions closer to the endfeet, soma, and process can be discerned by their mechanical properties. The local variation in the mechanical compliance along a single Müller cell may enable their diverse mechanical function in the retina. Müller cells protect neurons from a mechanical trauma by providing a soft mechanical buffering, mechano-sensing, and neurotrophic functions. We found that the observed elastic moduli of the endfeet and process in our study are higher than values reported in the other study (11). In addition, we found a different signature of local variations in mechanical compliances along a single Müller cell. We postulate that this difference may be partly attributed from the differences in contact stress provided by the AFM tip or by the different methodological approach. While we applied a static stress on a cell, others applied a high frequency stress (11). Thus, different constituents of cellular compartments can contribute to the values measured by different methodologies. We also postulate that this discrepancy can be partly caused by the difference in the origination of cells; we isolated Müller cells from rats but others from guinea pigs (11). In addition, there is a report that Müller cells from other regions of the retina differ in their structural characteristics (19).
In this study, we have investigated the local variations in the mechanical properties of rodent Müller cells using AFM-based biomechanics in vitro. The mechanical mapping of Müller cells may shed a light on the mechanism of retino-pathological processes and provide a key concept to understand the pathological dysfunctions involving Müller cells.
Materials and Methods
Experimental Animals
Fifteen adult Long-Evans rats (weight range, 250-350 g) of either sex were used. All animal care and experimental procedures were approved by the Institutional Animal Care and Use Committee. Experiments were carried out in accordance with the ARVO statement for the use of animals in Ophthalmic and Vision Research. Animals were deeply anesthetized with urethane (2 g/kg intraperitoneally). Retinas were dissected and immediately followed by the cell-isolation procedure.
Cell Isolation
We soaked freshly prepared retinal pieces in Ca2+- and Mg2+-free PBS with 0.05-0.1 mg/ml Papain (Sigma Aldrich, St. Louis, MO) for 30 min at 37°C and then washed them with PBS containing 200 units/ml DNase I (Sigma Aldrich, St. Louis, MO). In order to obtain isolated cells, the tissue pieces were gently rubbed by a pipette. After collecting the supernatant, PBS was replaced by a physiological salt solution (PSS; 136 mM NaCl/ 3 mM KCl/1 mM MgCl2/2 mM CaCl2/10 mM Hepes/10 mM D-glucose). The pH of the solution was adjusted to 7.4 by using 1M Tris buffer.
AFM measurements
All AFM measurements of cells placed on pre-cleaned glass substrates were taken with Autoprobe CP atomic force microscope (Park Scientific Instruments, Sunnyvale, CA) in liquid environment. During AFM measurements, a small amount of the medium solution was provided periodically through the inlet of the liquid cell (Park Scientific Instruments). The data collection was carried out only for the first three hours after starting a measurement to ensure the healthiness of the cells. A polystyrene bead (Seradyn Particle Technology, Indianapolis, IN) glued to commercial cantilevers (Microlevers, Veeco Probes, Camarillo, CA) were used to obtain a well-defined contact area, and to reduce the stress from otherwise sharp AFM tips (17). The cleanliness and the radius of the modified probe tip (1.5-4 μm) were verified by the reverse AFM topographic image. The force constant of each cantilever (0.02-0.06 N/m) was calibrated against a cantilever with a known force constant. The calibration cantilever was selected when the force constants from three different calibration methods agreed within 5% (20). These three methods involve the calibration with a commercial cantilever of a known force constant (0.157 N/m, TM Microscopes), the thermal fluctuations method, and the resonant frequency method. In order to obtain the elastic moduli, the nano-indentation experiments were performed by acquiring the f-d curves with a one-second time interval, i.e., 1 Hz, with the trigger force (1 nN - 2 nN). As a control experiment, f-d curves were obtained from a glass slide before taking measurements from the cells to make sure of the linear increase in force on a hard substrate as a function of the z-piezo displacement. At least 10 experiments were performed. The experimental details are described in our previous publications (17, 21).
Data Analysis
The force f on a cell and the indentation δ were used to generate f-δ curves by calculating the indentation and the force from the obtained z-piezo displacements and cantilever deflections. The indentations δ were calculated as the subtraction of the cantilever deflections from the scanner displacements. The applied force f was calculated by multiplying the force constant k with the cantilever deflection. The contact point between the tip and the sample was determined as the point where the slope of the force curve initially deviates from zero. The Hertz model was applied to determine the elastic moduli from f-δ curves according to Eq.1.
(1)
The f-δ curve is converted to the curve of elastic constant K =E/(1-ν2) versus the dimensionless quantity δ/R, where E is the Young's Modulus, R is the radius of the spherical tip, and ν (=0.33) is the Poisson ratio of the sample. The elastic constant K was obtained when it remains nearly constant as δ/R varies as would be expected for linear homogenous samples.
Acknowledgements
This work was supported by National Research Foundation of Korea Grant funded by Korean Government (NRF-2012R1A1A1015282) and by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (2013R1A1A3008608).
Competing Interests
The authors have declared that no competing interest exists.
References
1. Parpura V, Verkhratsky A. Neuroglia at the crossroads of homoeostasis, metabolism and signalling: evolution of the concept. ASN Neuro. 2012;4(4):201-5
2. Newman E, Reichenbach A. The Muller cell: A functional element of the retina. Trends Neurosci. 1996;19(8):307-12
3. Reichenbach A, Bringmann A. New functions of Muller cells. Glia. 2013;61(5):651-78
4. Reichenbach A, Hagen E, Schippel K, Bruckner G, Reichelt W, Leibnitz L. Cytotopographical specialization of enzymatically isolated rabbit retinal Muller (glial) cells: structure, ultrastructure, and 3H-ouabain binding sites. Z Mikrosk Anat Forsch. 1988;102(6):897-912
5. Reichenbach A, Hagen E, Schippel K, Eberhardt W. Quantitative electron microscopy of rabbit Muller (glial) cells in dependence on retinal topography. Z Mikrosk Anat Forsch. 1988;102(5):721-55
6. Panozzo G, Mercanti A. Optical coherence tomography findings in myopic traction maculopathy. Arch Ophthalmol. 2004;122(10):1455-60
7. Gaucher D, Haouchine B, Tadayoni R, Massin P, Erginay A, Benhamou N. et al. Long-term follow-up of high myopic foveoschisis: natural course and surgical outcome. Am J Ophthalmol. 2007;143(3):455-62
8. Felmy F, Pannicke T, Richt JA, Reichenbach A, Guenther E. Electrophysiological properties of rat retinal Muller (glial) cells in postnatally developing and in pathologically altered retinae. Glia. 2001;34(3):190-9
9. Francke M, Faude F, Pannicke T, Bringmann A, Eckstein P, Reichelt W. et al. Electrophysiology of rabbit Muller (glial) cells in experimental retinal detachment and PVR. Investigative Ophthalmology & Visual Science. 2001;42(5):1072-9
10. Pannicke T, Wolfgang F, Biedermann B, Schadlich H, Grosche J, Faude F. et al. P2X(7) receptors in Muller glial cells from the human retina. J Neurosci. 2000;20(16):5965-72
11. Lu YB, Franze K, Seifert G, Steinhauser C, Kirchhoff F, Wolburg H. et al. Viscoelastic properties of individual glial cells and neurons in the CNS. Proc Natl Acad Sci U S A. 2006;103(47):17759-64
12. Wang X, Xu GZ, Fan JW, Zhang M. Mechanical stretching induces matrix metalloproteinase-2 expression in rat retinal glial (Muller) cells. Neuroreport. 2013;24(5):224-8
13. Heidemann SR, Wirtz D. Towards a regional approach to cell mechanics. Trends Cell Biol. 2004;14(4):160-6
14. Discher D, Dong C, Fredberg JJ, Guilak F, Ingber D, Janmey P. et al. Biomechanics: Cell Research and Applications for the Next Decade. Ann Biomed Eng. 2009;37(5):847-59
15. Suresh S. Biomechanics and biophysics of cancer cells. Acta Mater. 2007;55(12):3989-4014
16. Kuznetsova TG, Starodubtseva MN, Yegorenkov NI, Chizhik SA, Zhdanov RI. Atomic force microscopy probing of cell elasticity. Micron. 2007;38(8):824-33
17. Park S, Koch D, Cardenas R, Kas J, Shih CK. Cell motility and local viscoelasticity of fibroblasts. Biophys J. 2005;89(6):4330-42
18. Mahaffy RE, Shih CK, MacKintosh FC, Kas J. Scanning probe-based frequency-dependent microrheology of polymer gels and biological cells. Phys Rev Lett. 2000;85(4):880-3
19. Franze K, Francke M, Gunter K, Christ AF, Korber N, Reichenbach A. et al. Spatial mapping of the mechanical properties of the living retina using scanning force microscopy. Soft Matter. 2011;7(7):3147-54
20. Mahaffy RE, Park S, Gerde E, Kas J, Shih CK. Quantitative analysis of the viscoelastic properties of thin regions of fibroblasts using atomic force microscopy. Biophys J. 2004;86(3):1777-93
21. Lee YJ, Patel D. and Park S. Local Rheology of Human Neutrophils Investigated Using Atomic Force Microscopy. International Journal of Biological Sciences. 2011;7(1):102-11
Author contact
![]() Corresponding author: Soyeun Park. Department of Physics, Texas Tech University, Box 41051, Lubbock, TX 79409. Email: sypark20com. Current address: College of Pharmacy, Keimyung University, Daegu, 704-701, South Korea.
Corresponding author: Soyeun Park. Department of Physics, Texas Tech University, Box 41051, Lubbock, TX 79409. Email: sypark20com. Current address: College of Pharmacy, Keimyung University, Daegu, 704-701, South Korea.

 Global reach, higher impact
Global reach, higher impact