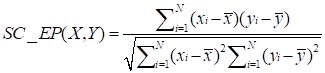Impact Factor
ISSN: 1449-2288
Int J Biol Sci 2018; 14(14):1950-1959. doi:10.7150/ijbs.28260 This issue Cite
Research Paper
Prediction of CircRNA-Disease Associations Using KATZ Model Based on Heterogeneous Networks
1. School of Computer Science, Shaanxi Normal University, Xi'an 710119, China
2. Department of Mechanical Engineering and Division of Biomedical Engineering, University of Saskatchewan, Saskatoon, SK S7N 5A9, Canada
Received 2018-7-2; Accepted 2018-9-30; Published 2018-11-1
Abstract
Circular RNAs (circRNAs) are a large group of endogenous non-coding RNAs which are key members of gene regulatory processes. Those circRNAs in human paly significant roles in health and diseases. Owing to the characteristics of their universality, specificity and stability, circRNAs are becoming an ideal class of biomarkers for disease diagnosis, treatment and prognosis. Identification of the relationships between circRNAs and diseases can help understand the complex disease mechanism. However, traditional experiments are costly and time-consuming, and little computational models have been developed to predict novel circRNA-disease associations. In this study, a heterogeneous network was constructed by employing the circRNA expression profiles, disease phenotype similarity and Gaussian interaction profile kernel similarity. Then, we developed a computational model of KATZ measures for human circRNA-disease association prediction (KATZHCDA). The leave-one-out cross validation (LOOCV) and 5-fold cross validation were implemented to investigate the effects of these four types of similarity measures. As a result, KATZHCDA model yields the AUCs of 0.8469 and 0.7936+/-0.0065 in LOOCV and 5-fold cross validation, respectively. Furthermore, we analyze the candidate association between hsa_circ_0006054 and colorectal cancer, and results showed that hsa_circ_0006054 may function as miRNA sponge in the carcinogenesis of colorectal cancer. Overall, it is anticipated that our proposed model could become an effective resource for clinical experimental guidance.
Keywords: CircRNA-disease association, similarity measure, KATZ model
Introduction
Circular RNAs (circRNAs) are a class of endogenous non-coding RNAs with a covalently closed continuous loop that lacks 5'-3' polarity structure. The first circRNA was found in 1976 in an electron microscopy-based study of RNA viruses [1]. Nonetheless, due to the structural specificity, unknown function and low abundance of circRNAs, they were initially assumed to be artefacts or mis-splicing products and did not attract much attention [2]. In recent years, thanks to the development of high-throughput sequencing technology and other techniques [3], an increasing number of circRNAs have been identified in thousands of living organisms including archaea, plants and animals [4-7]. The biogenesis mechanisms of circRNAs mainly include intron pairing-driven [8-10], lariat-driven [11], and RNA-binding protein-driven circularization [12]. In addition, circRNAs can regulate gene expression at transcriptional or post-transcriptional levels by titrating microRNAs (miRNAs), regulating transcription and interfering with splicing [13, 14]. CircRNAs play a critical role in biological processes including transcription, mRNA splicing, RNA decay and translation [15]. Therefore, the misregulation of circRNAs may cause abnormal cellular functions and growth defects and are involved in diseases.
Several circRNAs have been reported to be associated with human diseases, such as glioma tumorigenesis, osteosarcoma, colorectal cancer and so on. Circ-FBXW7 is reduced in glioblastoma clinical samples compared with their paired tumor-adjacent tissues, and circ-FBXW7 expression is also positively associated with glioblastoma patients overall survival [16]. circPVT1 is significantly up-regulated in the osteosarcoma tissues, and circPVT1 may be a biomarker for the diagnosis of osteosarcoma [17]. hsa_circ_0081001 is reported correlated with poor prognosis, and its expression level may dynamically monitor the condition changes of osteosarcoma [18]. Has_circ_001569 is highly expressed in cell proliferation and invasion of colorectal cancer, compared with non-cancerous samples [19]. Has_circ_0054633 is found to be upregulated in the peripheral blood of patients with type 2 diabetes, and it could be used as a candidate biomarker for the diagnosis for pre-diabetes and type 2 diabetes [20]. Upregulation or downregulation of circRNAs in specific disease tissues compared with normal samples could indicate their diagnostic potential to be new biomarkers. However, disease-related circRNAs are generally detected by analyzing RNA-seq or microarray data, then low throughput biological experiments are used to validate the abnormal expression such as RT-PCR, northern blot and so on. Furthermore, these experiments are expensive and time-consuming.
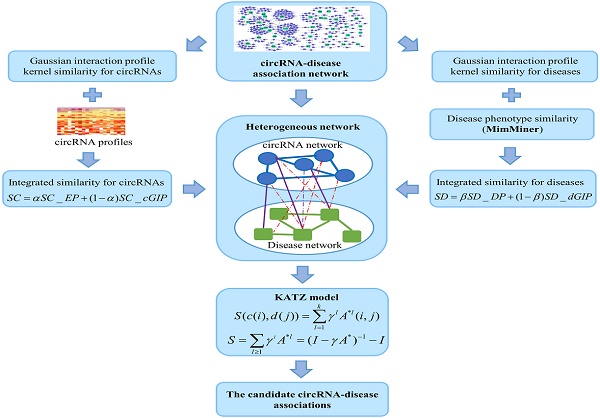
The CircR2Disease database is constructed, which collects experimentally validated circRNA-disease associations from published literatures [21]. Detecting the potential circRNA-disease associations is significant to understand the complex disease mechanism. To date, little efforts have made to develop the computational methods for circRNA-disease association prediction. Network-based models and machine learning methods have been widely applied to the prediction of bipartite biological associations. For example, KATZ measure is a network-based method to calculate the similarity between nodes in a heterogeneous network [22]. The KATZ measure has been successfully applied to social networks [23], and predict gene-disease associations [24], miRNA-disease associations [25, 26], lncRNA-disease associations [27] and microbe-disease associations [22]. Here, we propose a KATZ-based method for human circRNA-disease association prediction (KATZHCDA). In this study, the heterogeneous network is constructed by integrating known circRNA-disease associations, circRNA similarity network and disease similarity networks, where circRNA similarity is calculated from the circRNA expression and Gaussian interaction profiles (GIP) kernel while disease similarity is calculated from the disease phenotype and GIP kernel. By integrating the heterogeneous network and KATZ measure, the KATZHCDA model is developed to predict novel circRNA-disease associations.
To evaluate the performance of KATZHCDA model, the leave-one-out cross validation (LOOCV) and 5-fold cross validation (5-fold CV) are implemented. In addition, the prediction performance of different kinds of similarity measures are investigated. As a result, the KATZHCDA model achieved the best performance with AUCs of 0.8469 and 0.7936+/-0.0065 based on LOOCV and 5-fold cross validation, respectively. Finally, we analyze the candidate association between hsa_circ_0006054 and colorectal cancer, and results shown that hsa_circ_0006054 may be targeted by six miRNAs including hsa-miR-153, hsa-miR-194, hsa-miR-217, hsa-miR-431, hsa-miR-503, hsa-miR-646, and function as hsa-miR-217 sponge in the carcinogenesis of colorectal cancer. Overall, our framework is an effective resource for clinical experimental guidance.
Materials and Methods
Human circRNA-disease associations
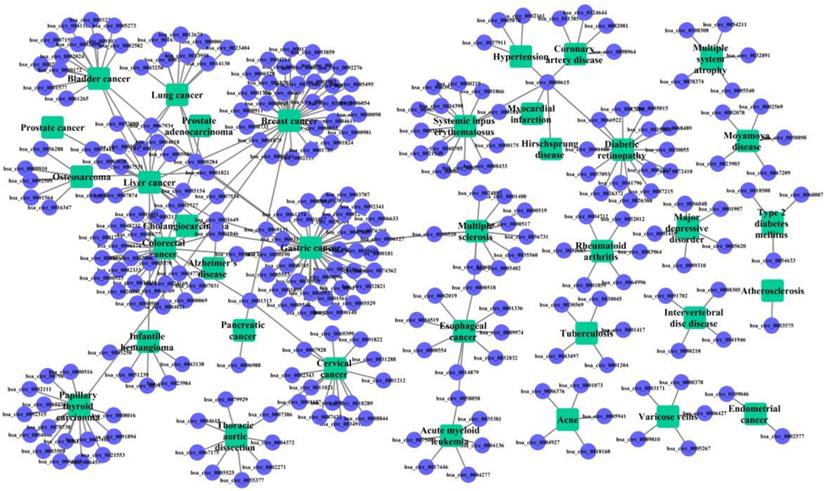
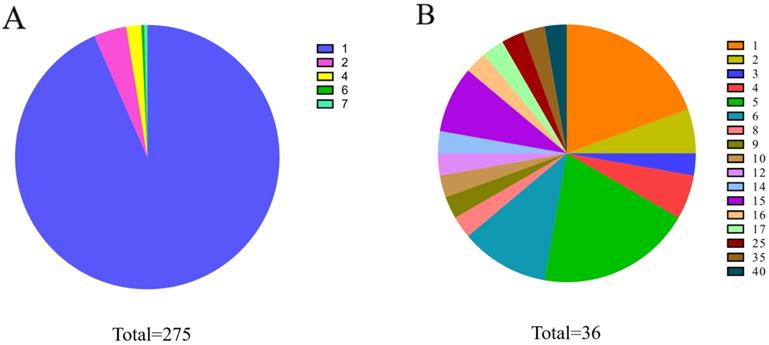
The known cricRNA-disease associations were derived from the CircR2Disease, which is a manually curated database for experimentally validated circRNA-disease associations. Here, we extract the circRNA-disease associations of human, in which the circRNAs own common circRNA ID with circBase and the diseases listed in the Online Mendelian Inheritance in Man (OMIM) [28, 29]. The gold standard dataset contains 312 distinct circRNA-disease associations involving 275 circRNAs and 36 diseases (Figure 1). The degree distributions of circRNAs and diseases in the bipartite of gold standard circRNA-disease association network are illustrated in Figure 2. The adjacency matrix A of gold standard circRNA-disease associations is constructed, and A(i,j) is equal to 1 when there is a known association between circRNA c(i) and disease d(j), otherwise 0.
CircRNA expression profile similarity
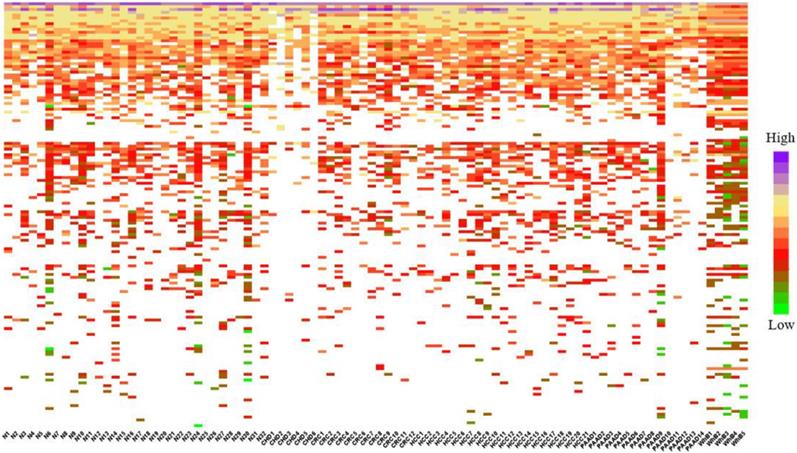
To calculate the similarity among circRNAs, we downloaded the expression profiles of circRNAs from exoRBase database (http://www.exorbase.org) [30]. After converting the circRNA ID of CircR2Disease into exoRBase, we obtained expression profile data for 149 circRNAs. Each record of circRNA expression profiles has 90 dimensions representing the expression levels based on RNA-seq data spanning normal individuals and patients with various diseases. A quick overview of the expression levels of 149 circRNAs in different kinds of samples is also shown (Figure 3). Based on the circRNA expression profiles, the Pearson correlation coefficient was used for similarity measurement, and a pair of circRNAs with a higher correlation score is considered to be more similar. Given expression profiles of two circRNAs denoted by X=(x1,..., xn) and Y=(y1,…,yn), then the Pearson correlation coefficient can be calculated as follows:
(1)
where xi and yi represent the expression values of two circRNAs in different human tissues or cell lines respectively, N denotes the number of components in the circRNA expression profiles.
Disease phenotype similarity
The disease phenotype similarity was downloaded from MimMiner [31], which measure disease similarity by computing similarity between Mesh terms appearing in the phenotype descriptions of diseases from OMIM database [32]. Here, let SD_DP represent the disease phenotype similarity matrix in gold standard dataset, in which each entry is the phenotype similarity score between diseases d(i) and d(j).
GIP kernel similarity
Based on assumption that similar circRNAs exhibit a similar interaction or non-interaction with the diseases and vice versa, the GIP kernel is used to measure the topology similarity for circRNAs and diseases as follows [33]:
(2)
(3)
where c(i) denotes the binary vector encoding the presence or absence with each disease, i.e., the i-th row of the adjacency matrix A. nc denotes the number of circRNAs. Similarly, d(i) denotes the binary vector encoding the presence or absence with each circRNAs according to the i-th column of the adjacency matrix A. nd denotes the number of diseases.
Bipartite graph of the circRNA-disease associations. The rectangles represent the diseases, and the circles represent the circRNAs. An edge corresponds to the gold standard circRNA-disease associations.
Pie graph of degree distribution for circRNAs or diseases. (A) Degree proportion of circRNAs. (B) Degree proportion of diseases.
Heatmap of circRNAs in different samples.
Integrated similarity for circRNAs and diseases
The circRNA expression profile similarity and disease phenotype similarity cannot cover all the circRNAs and diseases in the gold standard dataset. Therefore, the GIP kernel similarity for circRNAs and diseases were integrated based on known circRNA-disease associations. Finally, the circRNA similarity matrix was calculated by integrating circRNA expression profile similarity (SC_EP) and GIP kernel similarity (SC_cGIP) for circRNAs as in Equation (4), and the disease similarity matrix was computed by integrating the disease phenotype similarity (SD_DP) and GIP kernel similarity (SD_dGIP) for diseases as in Equation (5).
(4)
(5)
KATZHCDA
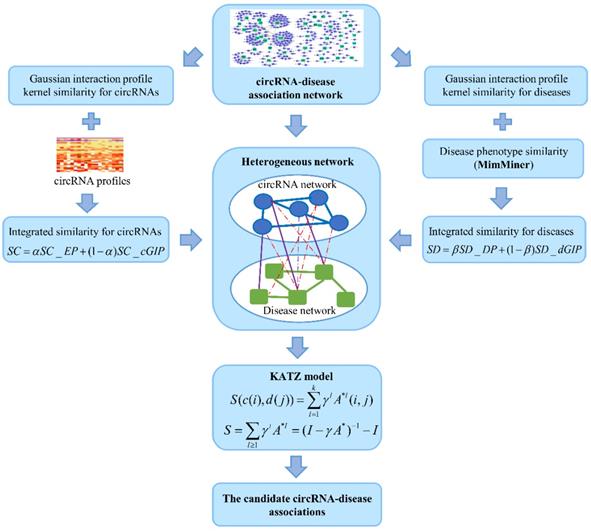
KATZ measure is a graph-based method to calculate the similarity between nodes in a heterogeneous network [23]. The number of walks between nodes and walk length are considered to be two effective similarity metrics in the network. So, counting the number of walks of different lengths between circRNA node and disease node can be used to measure the circRNA-disease associations. Here, heterogeneous network is constructed by integrating the circRNA similarity network, disease similarity network and the known circRNA-disease associations (Figure 4). However, with the variation of parameters α and β, the heterogeneous network is also changed. Anyway, the adjacency matrix of the heterogeneous network could be denoted as follows:
(6)
where SC represents the adjacency matrix of circRNA similarity network, SD represents the disease similarity network, A represents the adjacency matrix of known circRNA-disease associations.
Based on the known circRNA-disease association adjacency matrix, the number of walks of length l between circRNA ci and disease dj can be calculated by computing Al(i,j). Furthermore, heterogeneous network A* can be used for the prediction of new circRNA-disease associations. To get a single measurement of each circRNA-disease pair, all walks of different lengths are integrated. Because different lengths of walks have different contribution, a nonnegative parameter γ is introduced to dampen the contribution of longer walks. Therefore, the potential associations between circRNA ci and disease dj could be calculated by:
(7)
All walks of network can be shown as:
(8)
where S represents the similarities of all the circRNA-disease pairs. However, it is not necessary to consider all the path lengths. Path of longer lengths in sparse circRNA-disease network may be insignificant or meaningless. Therefore, we set k to be 2, 3 and 4, and the final prediction scores for potential associations are calculated.
The flowchart of the KATZHCDA model.
Experiments and Results
Performance evaluation
The LOOCV and 5-fold CV are implemented on the gold standard human circRNA-disease associations in CircR2Disease database to evaluate the performance of KATZHCDA model. In each round of LOOCV, a known circRNA-disease pair is removed in turn as test sample and the other known circRNA-disease pairs are used as training samples. Then, the receiver operating characteristic (ROC) curve is used to evaluate the prediction performance of KATZHCDA model, which plots the true positive rate (TPR, sensitivity) against false positive rate (FPR, 1-specificity) over various score thresholds. Here, sensitivity (SEN) refers to the percentage of positive cases that are correctly identified, and specificity (SPE) means the percentage of negative cases that are correctly predicted. In this way, the area under the curve (AUC) is calculated from the corresponding area under ROC curve. In addition, in the framework of 5-fold CV, the gold standard human circRNA-disease associations are randomly divided into five equal size subjects. One of them is retained as testing samples while the remaining datasets are regarded as training samples in turns. This process randomly repeated 100 times, and the average AUC values and standard deviations were obtained.
Effect of parameters
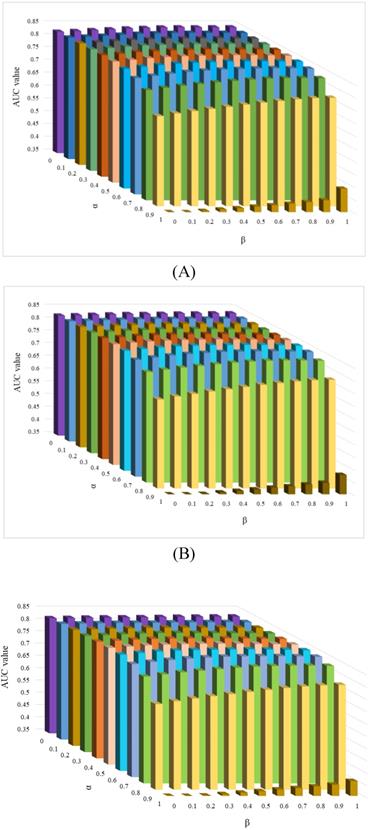
There are four parameters in the KATZHCDA model, including the α and β, the number of walks k and nonnegative parameter γ. When α(β)=1, only circRNA expression profile similarity matrix (disease phenotype similarity) was considered. While when α(β)=0, only topology similarity of known circRNA-disease network was used. To evaluate the performances with different types of similarity matrices, various values were set for α and β. Here, when the values of α and β take 0, 0.1, …, 0.9, 1, the values of LOOCV AUC were calculated. In addition, based on the suggestion by Zou et al., γ is selected on the basis of γ < 1/||A||2 [26]. Therefore, γ is set as 0.01 by following precious studies [22]. Furthermore, k is another parameter that have a very large influence on the prediction results for circRNA-disease associations. Because of the circRNA-disease network is very sparse, so too long walks may be meaningless. Here, we implement a series of comparison experiments to evaluate the performance of KATZHCDA by adjusting the parameter k. LOOCV was implemented when k was set as 2, 3, 4 (Figure 5). The highest LOOCV AUC values were 0.8469 (α=0.5, β=0.8), 0.8443 (α=0.6, β=0.7), and 0.8438 (α=0.6, β=0.7) when k was set from 2 to 4, respectively. As a result, we found the LOOCV AUC value of this model are highest when α, β and k was set as 0.5, 0.8 and 2, respectively. Because little gap between these highest LOOCV AUC values, 5-fold CV was also implemented (Table 1). Results showed that the average AUC values keep an increasing trend when k increased from 2 to 4. Based on the opposite trend of LOOCV and 5-fold, we infer it may be caused by the 5-fold CV each round was removed too many effective edges of the heterogeneous network and the longer walks maybe make up this shortcoming. Therefore, we set α as 0.5 and β as 0.8 in the following analysis.
Effect of parameter α and β when k was set as 2, 3 and 4.
5-fold CV experimental results of setting parameter k.
| 5-fold CV (Average AUC) | k = 2 | k = 3 | k = 4 |
|---|---|---|---|
| α=0.5, β=0.8 | 0.7616+/-0.0062 | 0.7764+/-0.0066 | 0.7833+/-0.0075 |
| α=0.6, β=0.7 | 0.7561+/-0.0067 | 0.7710+/-0.0070 | 0.7763+/-0.0065 |
Comparison with different similarity measures
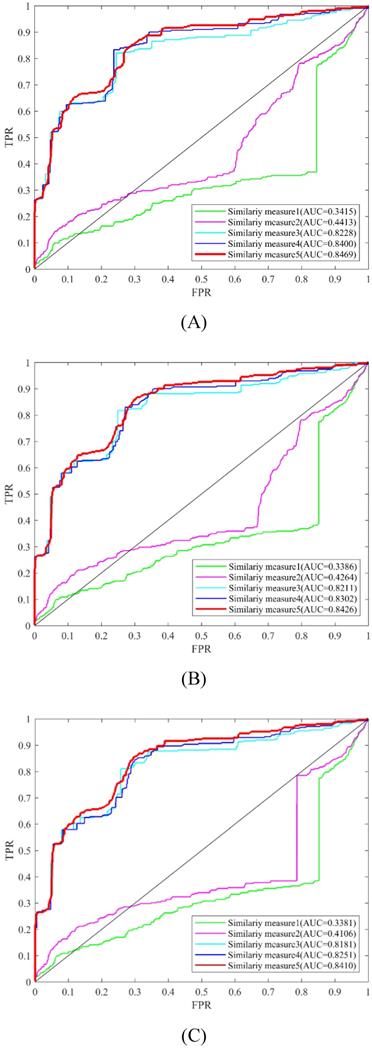
In this study, different kinds of information were used to measure the similarity of circRNAs and diseases. These types of similarity measures conclude circRNA expression profile similarity, disease phenotype similarity, GIP kernel similarity. In order to evaluate the usefulness of these similarity measures, LOOCV and 5-fold were implemented to compare the experimental results (Table 2, Figure 6). From the LOOCV results, we obtained the highest AUC of 0.8469 by integrating the circRNA expression profile similarity, disease phenotype similarity, GIP kernel similarity for circRNAs and diseases. However, the highest average AUC of 0.7936 by integrating disease phenotype similarity and GIP kernel similarity for circRNAs in 5-fold CV. In both LOOCV and 5-fold CV, the experiment results showed that GIP kernel similarity for circRNAs and diseases are very effective for the prediction of circRNA-disease associations.
Candidate circRNA for the specific disease
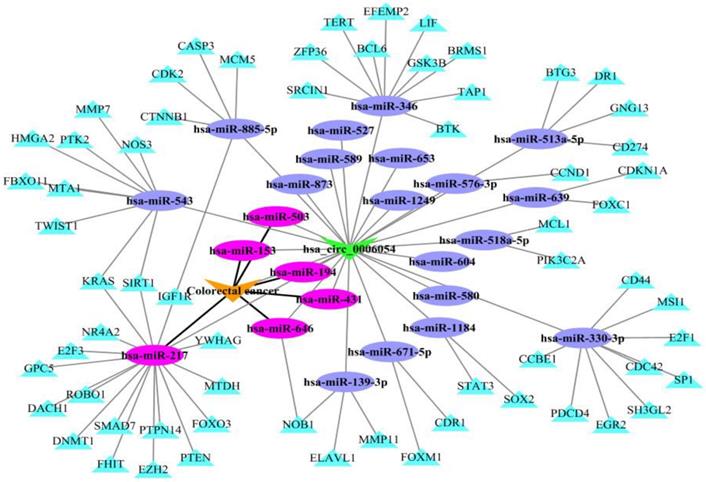
To illustrate the application of KATZHCDA model for the disease-associated circRNA prediction, the miRNA-circRNA and miRNA-disease associations are introduced. It has reported that circRNAs can act as competing endogenous RNAs (ceRNAs) to sequester miRNAs and prevent their interactions with target mRNAs [13]. Here, we analyze hsa_circ_0006054 as a putative candidate for playing a role in colorectal cancer as shown in Figure 7. Firstly, the potential miRNA targets on hsa_circ_0006054 are predicted with the TargetScan perl script, and strong experimentally validated miRNA targets are obtained from miRTarBase [34]. Then, the hsa_circ_0006054-miRNA-mRNA regulatory network is constructed. In addition, miRNA-related dysfunctions are widely associated with various diseases. Therefore, we download the experimentally verified miRNA-disease associations from HMDD [35], and mark the colorectal cancer related miRNAs in the hsa_circ_0006054-miRNA-mRNA network. The results showed that hsa_circ_0006054 may be targeted by six miRNAs including hsa-miR-153, hsa-miR-194, hsa-miR-217, hsa-miR-431, hsa-miR-503, hsa-miR-646, and function as hsa-miR-217 sponge in the carcinogenesis of colorectal cancer.
Prediction performance of KATZHCDA model with different similarity measures in the framework of LOOCV. (A) Performance comparison among five similarity measures when k was set as 2. (B) Performance comparison among five similarity measures when k was set as 3. (C) Performance comparison among five similarity measures when k was set as 4.
5-fold CV experimental results with different similarity measures.
| Similarity measures | 5-fold CV (k=2) | 5-fold CV (k=3) | 5-fold CV (k=4) |
|---|---|---|---|
| Similarity measure1 (α=1, β=0) | 0.3256+/-0.0092 | 0.3184+/-0.0111 | 0.3922+/-0.0110 |
| Similarity measure2 (α=1, β=1) | 0.4258+/-0.0120 | 0.4106+/-0.0097 | 0.3914+/-0.0099 |
| Similarity measure3 (α=0, β=0) | 0.7405+/-0.0077 | 0.7659+/-0.0079 | 0.7786+/-0.0070 |
| Similarity measure4 (α=0, β=1) | 0.7647+/-0.0060 | 0.7799+/-0.0067 | 0.7936+/-0.0065 |
| Similarity measure5 (α=0.5, β=0.8) | 0.7616+/-0.0062 | 0.7764+/-0.0066 | 0.7833+/-0.0075 |
The hsa_circ_0006054-miRNA-mRNA network in colorectal cancer.
Discussion and Conclusion
Increasing evidences show circRNAs are closely correlated with different type of diseases such as atherosclerosis [36], Lung adenocarcinoma [37] and so on. Several investigations have been carried out to study the specifically dysregulated circRNA with diseases, which are regarded as biomarkers for disease diagnosis, therapeutic and prognosis. Upregulation and downregulation of circRNAs could be detected by high throughput RNA sequencing techniques in disease tissues compared with adjacent tissues. Based on these biological techniques, disease-related circRNA databases have laid a significant foundation for the research of circRNA functions. Of these databases, circR2Disease database manually collected the experimentally validated circRNA-disease associations [21]. However, little computational models have constructed for predicting potential circRNA-disease associations. Based on the assumption that circRNAs with similar functions tend to get involved in similar disease association patterns while similar diseases are more likely associated with the abnormal abundance of functional similar circRNAs. In this study, circRNA expression profiles, disease-phenotype similarity matrix, and known circRNA-disease associations were integrated to construct the heterogeneous network. Furthermore, because the heterogeneous network is very sparsity, GIP kernel similarities for circRNAs and diseases are also added to measure the similarities of circRNA-circRNA and disease-disease pairs. Then, KATZ model was used to measure the associations between circRNAs and diseases by integrating the walks with different lengths in the circRNA-disease heterogeneous network. The experimental results showed that KATZHCDA model could become an effective computation tool to predict the circRNA-disease associations.
The good performance of KATZHCDA mainly attributes to the following aspects. Firstly, the application of KATZ model guaranteed the basic effectiveness of our proposed method. The KATZ model employs the simple measure on the heterogeneous network, and succeed in predicting disease-related biological molecules. Secondly, reliable biological datasets are used to establish the circRNA similarity network and disease similarity network. Furthermore, KATZHCDA can predict the scores between circRNA and diseases simultaneously for all diseases. Hence, KATZHCDA is a useful biomedical resource for circRNA-disease association identification.
Despite the effectiveness of KATZHCDA model, it should be noted that KATZHCDA still has some limitations. First, the model mainly depends on the known circRNA-disease associations, which may cause possible bias by imbalanced training samples. The parameters were also influenced by the sparsity of the associations. With the addition of more links between circRNAs and diseases, the model may obtain higher prediction scores. Moreover, other kinds of information of circRNAs or diseases could be integrated to improve the predictive performance, such as miRNA-based circRNA similarity, circRNA-protein similarity, disease semantic similarity and so on. In addition, KATZHCDA is not applicable to predict novel circRNA-disease associations that without any known associations. Therefore, integrating more data sources and appropriate algorithms would improve the predictive performance.
Abbreviations
circRNAs: circular RNAs; miRNAs: microRNAs; GIP: Gaussian interaction profiles; LOOCV: leave-one-out cross validation; 5-fold CV: 5-fold cross validation; OMIM: Online Mendelian Inheritance in Man; ROC: receiver operating characteristic; TPR: true positive rate; FPR: false positive rate; SEN: sensitivity; SPE: specificity; AUC: area under the curve; ceRNAs: competing endogenous RNAs.
Acknowledgements
This paper is supported by the National Natural Science Foundation of China [Grant numbers 61672334, 61502290 and 61401263]. The funding agencies had no role in study, its design, the data collection and analysis, the decision to publish, or the preparation of the manuscript.
Competing Interests
The authors have declared that no competing interest exists.
References
1. Sanger HL, Klotz G, Riesner D, Gross HJ, Kleinschmidt AK. Viroids are single-stranded covalently closed circular RNA molecules existing as highly base-paired rod-like structures. Proceedings of the National Academy of Sciences of the United States of America. 1976;73:3852-6
2. Nigro JM, Cho KR, Fearon ER, Kern SE, Ruppert JM, Oliner JD. et al. Scrambled exons. Cell. 1991;64:607-13
3. Zeng X, Lin W. A comprehensive overview and evaluation of circular RNA detection tools. Plos Computational Biology. 2017;13:e1005420
4. Danan M, Schwartz S, Edelheit S, Sorek R. Transcriptome-wide discovery of circular RNAs in Archaea. Nucleic acids research. 2012;40:3131-42
5. Chu Q, Zhang X, Zhu X, Liu C, Mao L, Ye C. et al. PlantcircBase: A Database for Plant Circular RNAs. Molecular plant. 2017;10:1126-8
6. Memczak S, Jens M, Elefsinioti A, Torti F, Krueger J, Rybak A. et al. Circular RNAs are a large class of animal RNAs with regulatory potency. Nature. 2013;495:333-8
7. Chen L, Huang C, Wang X, Shan G. Circular RNAs in Eukaryotic Cells. Current genomics. 2015;16:312-8
8. Ashwal-Fluss R, Meyer M, Pamudurti NR, Ivanov A, Bartok O, Hanan M. et al. circRNA biogenesis competes with pre-mRNA splicing. Molecular cell. 2014;56:55-66
9. Liang D, Wilusz JE. Short intronic repeat sequences facilitate circular RNA production. Genes & development. 2014;28:2233-47
10. Zhang XO, Wang HB, Zhang Y, Lu X, Chen LL, Yang L. Complementary sequence-mediated exon circularization. Cell. 2014;159:134-47
11. Barrett SP, Wang PL, Salzman J. Circular RNA biogenesis can proceed through an exon-containing lariat precursor. Elife. 2015;4:e07540
12. Conn SJ, Pillman KA, Toubia J, Conn VM, Salmanidis M, Phillips CA. et al. The RNA binding protein quaking regulates formation of circRNAs. Cell. 2015;160:1125-34
13. Hansen TB, Jensen TI, Clausen BH, Bramsen JB, Finsen B, Damgaard CK. et al. Natural RNA circles function as efficient microRNA sponges. Nature. 2013;495:384-8
14. Qu S, Yang X, Li X, Wang J, Gao Y, Shang R. et al. Circular RNA: A new star of noncoding RNAs. Cancer letters. 2015;365:141-8
15. Wang M, Yu F, Wu W, Zhang Y, Chang W, Ponnusamy M. et al. Circular RNAs: A novel type of non-coding RNA and their potential implications in antiviral immunity. International journal of biological sciences. 2017;13:1497-506
16. Yang Y, Gao X, Zhang M, Yan S, Sun C, Xiao F. et al. Novel Role of FBXW7 Circular RNA in Repressing Glioma Tumorigenesis. Journal of the National Cancer Institute. 2018:110
17. Kun-Peng Z, Xiao-Long M, Chun-Lin Z. Overexpressed circPVT1, a potential new circular RNA biomarker, contributes to doxorubicin and cisplatin resistance of osteosarcoma cells by regulating ABCB1. International journal of biological sciences. 2018;14:321-30
18. Kun-Peng Z, Chun-Lin Z, Jian-Ping H, Lei Z. A novel circulating hsa_circ_0081001 act as a potential biomarker for diagnosis and prognosis of osteosarcoma. International journal of biological sciences. 2018;14:1513-20
19. Xie H, Ren X, Xin S, Lan X, Lu G, Lin Y. et al. Emerging roles of circRNA_001569 targeting miR-145 in the proliferation and invasion of colorectal cancer. Oncotarget. 2016;7:26680-91
20. Zhao Z, Li X, Jian D, Hao P, Rao L, Li M. Hsa_circ_0054633 in peripheral blood can be used as a diagnostic biomarker of pre-diabetes and type 2 diabetes mellitus. Acta diabetologica. 2017;54:237-45
21. Fan C, Lei X, Fang Z, Jiang Q, Wu FX. CircR2Disease: a manually curated database for experimentally supported circular RNAs associated with various diseases. Database: the journal of biological databases and curation. 2018:2018
22. Chen X, Huang YA, You ZH, Yan GY, Wang XS. A novel approach based on KATZ measure to predict associations of human microbiota with non-infectious diseases. Bioinformatics (Oxford, England). 2018;34:1440
23. Katz L. A new status index derived from sociometric analysis. Psychometrika. 1953;18:39-43
24. Singh-Blom UM, Natarajan N, Tewari A, Woods JO, Dhillon IS, Marcotte EM. Prediction and validation of gene-disease associations using methods inspired by social network analyses. PloS one. 2013;8:e58977
25. Qu Y, Zhang H, Liang C, Dong X. Katzmda: prediction of mirna-disease associations based on katz model. IEEE Access. 2018;6:3943-50
26. Zou Q, Li J, Hong Q, Lin Z, Wu Y, Shi H. et al. Prediction of MicroRNA-Disease Associations Based on Social Network Analysis Methods. BioMed research international. 2015;2015:810514
27. Chen X. KATZLDA: KATZ measure for the lncRNA-disease association prediction. Scientific reports. 2015;5:16840
28. Glazar P, Papavasileiou P, Rajewsky N. circBase: a database for circular RNAs. RNA (New York, NY). 2014;20:1666-70
29. Hamosh A, Scott AF, Amberger JS, Bocchini CA, McKusick VA. Online Mendelian Inheritance in Man (OMIM), a knowledgebase of human genes and genetic disorders. Nucleic acids research. 2005;33:D514-7
30. Li S, Li Y, Chen B, Zhao J, Yu S, Tang Y. et al. exoRBase: a database of circRNA, lncRNA and mRNA in human blood exosomes. Nucleic acids research. 2017;46:D106-D12
31. van Driel MA, Bruggeman J, Vriend G, Brunner HG, Leunissen JA. A text-mining analysis of the human phenome. European journal of human genetics: EJHG. 2006;14:535-42
32. Lipscomb CE. Medical Subject Headings (MeSH). Bulletin of the Medical Library Association. 2000;88:265-6
33. van Laarhoven T, Nabuurs SB, Marchiori E. Gaussian interaction profile kernels for predicting drug-target interaction. Bioinformatics (Oxford, England). 2011;27:3036-43
34. Chou CH, Shrestha S, Yang CD, Chang NW, Lin YL, Liao KW. et al. miRTarBase update 2018: a resource for experimentally validated microRNA-target interactions. Nucleic acids research. 2018;46:D296-d302
35. Li Y, Qiu C, Tu J, Geng B, Yang J, Jiang T. et al. HMDD v2.0: a database for experimentally supported human microRNA and disease associations. Nucleic acids research. 2014;42:D1070-4
36. Burd CE, Jeck WR, Liu Y, Sanoff HK, Wang Z, Sharpless NE. Expression of linear and novel circular forms of an INK4/ARF-associated non-coding RNA correlates with atherosclerosis risk. PLoS genetics. 2010;6:e1001233
37. Zhao J, Li L, Wang Q, Han H, Zhan Q, Xu M. CircRNA Expression Profile in Early-Stage Lung Adenocarcinoma Patients. Cellular physiology and biochemistry: international journal of experimental cellular physiology, biochemistry, and pharmacology. 2017;44:2138-46
Author contact
![]() Corresponding author: Xiujuan Lei, School of Computer Science, Shaanxi Normal University, Xi'an 710119, China. Email: xjleiedu.cn
Corresponding author: Xiujuan Lei, School of Computer Science, Shaanxi Normal University, Xi'an 710119, China. Email: xjleiedu.cn

 Global reach, higher impact
Global reach, higher impact